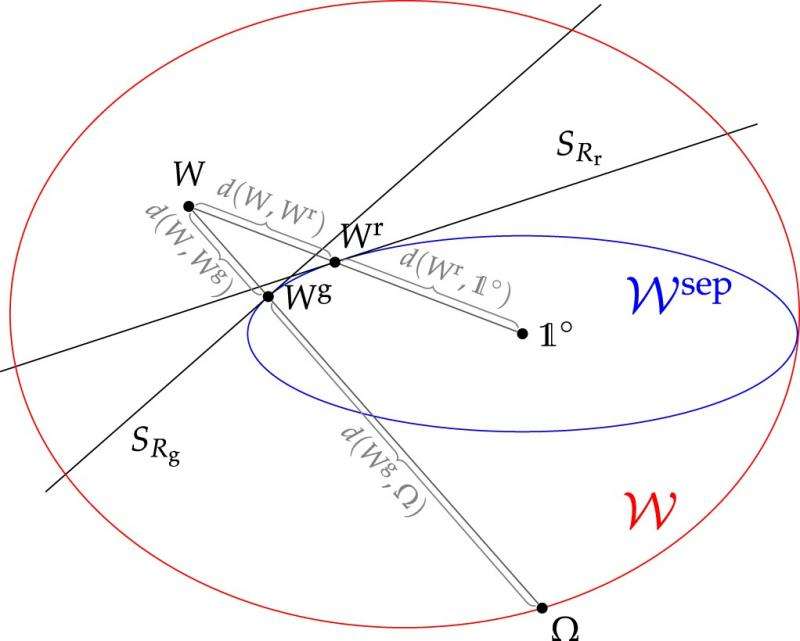
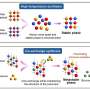
This figure illustrates the test for causal nonseparability, which can determine whether any quantum processes is causally nonseparable. Credit: Araújo, et al.
(Phys.org)—In a quantum superposition, a quantum object can be in two incompatible states at the same time, which is famously illustrated by Schrödinger's dead-and-alive cat. Recent research has shown that it's possible to have a superposition not only of incompatible states, but also of incompatible orders of events. We often think of events occurring in a definite chronological order, with event A happening (and causing) event B, or vice versa. But in certain quantum processes, events don't happen in a single definite order, but instead both orders (A before B, and B before A) occur at the same time. This counterintuitive superposition-like phenomenon is called "causal nonseparability."
"In everyday life, we are used to experiencing one thing always happening after another, effects following their causes," Mateus Araújo at the University of Vienna and the Institute for Quantum Optics and Quantum Information in Vienna, Austria, told Phys.org. "So it is a bit unsettling to realize that deep down Nature doesn't work like this, that things can happen without a definite causal order, where we cannot say what is the cause and what is the effect."
Until now, causal nonseparability in quantum mechanics has been conceived only in a very abstract way, with no clear physical interpretation. But in a new paper published in the New Journal of Physics, Araújo and coauthors have described an example of a physical quantum process that demonstrates causal nonseparability.
"The theory of relativity has already shaken the idea that there is an absolute, global time, and that everyone experiences the flow of time and time relations in the same way: two different observers in different reference frames may, for instance, disagree on which event happens before the other," said coauthor Cyril Branciard at CNRS and the Universite Grenoble Alpes in Grenoble, France.
"Quantum theory, on the other hand, has shaken our understanding of reality by telling us that physical systems may not have well-defined properties, and may be in a 'superposition' of incompatible states. For example, a poor cat could be both alive and dead at the same time. Now we find that not just physical properties, but also causal relations (or causal orders) themselves can be undefined, and can be put in some kind of superposition—a phenomenon that had not been observed experimentally until very recently."
Quantum switch
The causally nonseparable quantum process that the physicists explore here is called a quantum switch, which was recently proposed as a way to improve the efficiency of quantum computers. In the new study, the physicists introduced a test for causal nonseparability, which they explain is similar to tests for quantum entanglement. Both types of tests produce a certain range of values if all operations are performed in the "classical" way (that is, using only causally separable resources or non-entangled states, respectively) but produce a different range of values if these conditions are not met.
The physicists showed that the causal nonseparability of not only the quantum switch, but of any causally nonseparable process, can be detected by their new test. This may make the test useful for identifying causal nonseparability in other systems that may be experimentally implemented in the future.
As the researchers explain, just because the quantum switch is causally nonseparable (meaning the operations do not follow a definite order), this does not mean that it violates any causal inequality (which would happen if a future event were to cause a past event). This is because there is no definite past or future in the quantum switch; neither event definitely comes before or after the other. Although the quantum switch does not violate any causal inequality, the question remains open as to whether any practical, physical process that can be experimentally realized may do so.
Causally nonseparable computing
Previous research has shown that the quantum switch has computational advantages over standard causally separable protocols, which suggests that causal nonseparability may have applications in quantum computing.
"The way quantum computers (or any device that performs some quantum information processing task) are studied typically assumes that the operations they perform are done in a definite order," Branciard said. "This is, for instance, a basic assumption of the standard 'circuit model' of quantum computation, which is commonly used to describe the functioning of quantum computers. Hence, the vast majority of results we know about the power of quantum computers (for example, what kinds of problems they can solve, with what efficiency, and the complexity of the algorithms they can run) apply only for cases with a definite causal order between all operations—in other words, for causally separable resources.
"The fact that quantum theory also allows for causally nonseparable resources (for example, the quantum switch) thus opens up new possibilities, and it is thus natural to expect that causally nonseparable resources can outperform causally separable ones for certain tasks."
An example of such a task, previously proposed by physicist Giulio Chiribella, involves determining whether the order of operations of a certain process matters: do you get the same result when you perform "A then B" as you do when performing "B then A"? If the result is the same, then the operations are said to commute; if not, they anticommute.
To answer this question, a causally separable process must perform both "A then B" and "B then A" orders and compare the results. On the other hand, a causally nonseparable process such as the quantum switch performs both orders simultaneously, in a quantum superposition, which solves the problem in one step. Not only is the nonseparable process more efficient, but in some cases it may be the only way to solve the problem—for instance, the "black boxes" used to perform the quantum operations may be destroyed after a single use, so that the procedure can only be performed once.
Since the quantum switch is the simplest example of causal nonseparability, the physicists hope that different kinds of causally nonseparable processes might allow for even stronger advantages over causally separable ones.
"More generally, I expect causally nonseparable processes to find applications in various other kinds of situations—just like entanglement proved to be useful for various applications in quantum information processing," Branciard said. "The full power of causal nonseparability is still to be discovered, and this makes this line of research particularly exciting!"
More information: Mateus Araújo, et al. "Witnessing causal nonseparability." New Journal of Physics. DOI: 10.1088/1367-2630/17/10/102001
Journal information: New Journal of Physics
© 2015 Phys.org