Can the brain map 'non-conventional' geometries (and abstract spaces)?
Grid cells, space-mapping neurons of the entorhinal cortex of rodents, could also work for hyperbolic surfaces. A SISSA study just published in Interface, the journal of the Royal Society, tests a model (a computer simulation) based on mathematical principles, that explains how maps emerge in the brain and shows how these maps adapt to the environment in which the individual develops.
"It took human culture millennia to arrive at a mathematical formulation of non-Euclidean spaces", comments SISSA neuroscientist Alessandro Treves, "but it's very likely that our brains could get there long before. In fact, it's likely that the brain of rodents gets there very naturally every day".
Treves coordinated a study just published in the journal Interface. Euclidean geometry is the kind of geometry we normally study at school, whereas non-Euclidean geometries are all those that reject one or more of Euclid's five postulates. A geometry that unfolds on a curved surface is an example. Recent research has investigated how the brain encodes flat spaces. In 2005, Edvard and May-Britt Moser discovered grid cells, neurons of the entorhinal cortex of rodents that fire in a characteristic way when the animal moves in an arena. The discovery has recently been awarded the Nobel Prize, but all experiments conducted to date have involved flat (Euclidean) surfaces. So what happens with other types of surface?
The starting point is the formation of these brain "maps". "There are two main classes of theoretical models that attempt to explain it, but both of them assume that our brain contains some kind of "engineer" that has prepared things appropriately" says Treves. "These models take for granted that the system originates with substantial prior knowledge, and they closely reproduce the behaviour of the biological system under known conditions, since they are constructed precisely on its observation. But what happens in conditions that have yet to be explored experimentally? Are these models able to 'generalize', that is, to make a genuine prediction to be then confirmed by other experiments? A correct theory should tell us more than what we already know".
Treves and colleagues have been developing a new, radically different model since 2005, and in their recent paper they have indeed attempted a broad generalization. "Ours is a self-organizing model, which simulates the behaviour of 'artificial' grid cells capable of learning by exploring the environment".
More in detail
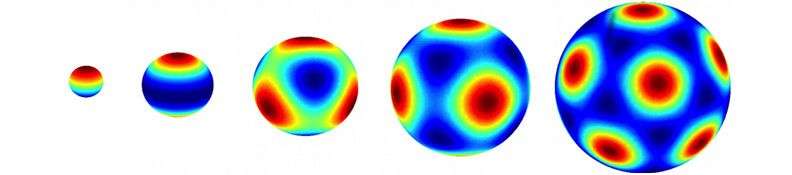
The model is based on mathematical rules and its final characteristics are determined by the environment in which it "learns from experience". In previous studies, the model was tested on flat surfaces: "in these settings our artificial grid cell shows the same hexagonal symmetrical firing pattern seen in biological cells".
"To apply it to a new situation, we thought of having our model move in a non-Euclidean space, and we chose the simplest setting: a space with a constant curvature, in other words a sphere or pseudosphere". The recently published study shows the results achieved with the pseudospherical surface, which demonstrate that in this case the firing pattern has a heptagonal, seven-point, symmetry. This finding can now easily be compared with the firing of real grid cells, in rodents raised on a pseudospherical surface. "We're waiting for the experimental results of our Nobel Prize-winning colleagues from Trondheim" explains Treves. "If our results are confirmed, then new theoretical considerations will ensue that will open up new lines of research".
In addition to demonstrating that maps adapt to the environment in which the individual develops (and so are not genetically predetermined), the observation of a heptagonal symmetry in new experimental conditions - which would show that the brain is able to encode a non-Euclidean space - would also suggest that grid cells might play a role in mapping many other types of space, "including abstract spaces", adds Treves. "Try to imagine what we might define as the space of movements, or the space of the different expressions of the human face, or shapes of a specific object, like a car: these are continuous spaces that could be mapped by cells that are not the same but are similar to grid cells, cells that could somehow represent the graph paper on which to measure these spaces".
More information: Can rodents conceive hyperbolic spaces? rsif.royalsocietypublishing.or … .1098/rsif.2014.1214
Journal information: Journal of the Royal Society Interface
Provided by International School of Advanced Studies (SISSA)