Generating Mobius strips of light: Researchers experimentally produce these structures from light polarization
A collaboration of researchers from Canada, Europe and the USA have experimentally produced Möbius strips from the polarization of light, confirming a theoretical prediction that it is possible for light's electromagnetic field to assume this peculiar shape.
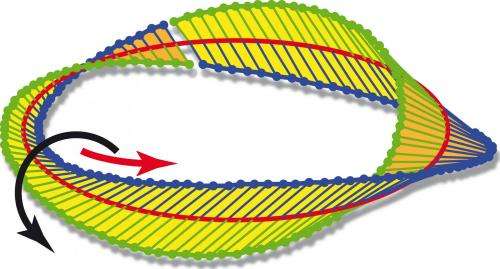
Möbius strips are easy to create. Take a strip of paper, twist it once and join up the ends. That's it, you have created a Möbius strip: a three dimensional structure that has only one side. Millions of school children do exactly this in classrooms every year. But finding Möbius strips occurring naturally is another issue.
"This is one of the very few known examples of a Möbius structure appearing in nature," states Robert W. Boyd, professor of optics and physics at the University of Rochester and the Canada Excellence Research Chair in Quantum Nonlinear Optics at the University of Ottawa. Boyd is one of the senior authors of the paper describing this research, which is published online by Science this week.
Demonstrating that a Möbius strip can be made of polarization states of light is interesting not only for improving the fundamental understanding of optical polarization but also because it could be used to generate complex structures at micro and nanoscales.
Light is an electromagnetic wave, and as such it has an electromagnetic field. The direction in which the electric component of this field oscillates is commonly referred to as the light's polarization. Polarization, for example, is the key to understanding glare-reducing polarized sunglasses and making 3D cinema possible. The polarization of sunlight beams is usually random, which means the orientation of the electric field is independent from one beam to another. But when light is reflected from many objects - for example water, glass, or a highway's surface - the reflected light becomes polarized in a specific direction, parallel to the surface that is reflecting the light. Polarized sunglasses are able to block light polarized in that direction, thereby greatly reducing the glare but letting other light through unobstructed.

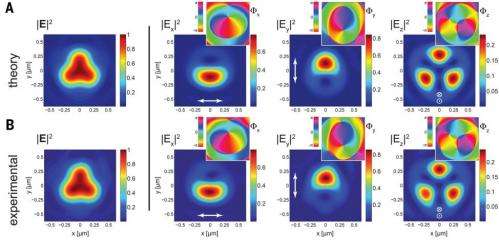
In their experiment, to produce these Möbius strips, the researchers use a specific, rather exotic, type of light beam: a tightly focused laser beam that they refer to as structured light. Structured light has a very specific polarization and intensity distribution in the light beam - and therefore the electromagnetic field oscillates differently for different parts of the beam. It is not always at right angles to the direction the light is moving in, as would be the case in a standard laser beam. In this highly structured beam, there will be components of the electric field in all three dimensions. Moreover, different parts of the beam will have different electric field components in different directions.
To create the structured beam and measure its polarization, the researchers used a series of optical tools. The laser light is first passed through a q-plate - effectively a liquid crystal lens developed by Lorenzo Marrucci and Ebrahim Karimi in Naples. This creates the structured beam.
To image the polarization the researchers used a nanoparticle. This particle was scanned over the cross-section of the beam and the researchers observed the light it scattered. By determining how the light was scattered, and effectively using it as an interferometer, the polarization of the light beam at the focus is detected, and consequently the Möbius strips emerge. This procedure was developed by Gerd Leuchs and Peter Banzer in Erlangen.
The Möbius strips show how the electric field is oriented at each position on a circular path surrounding the axis of the laser beam. Depending on the particulars of the structure of laser beam, the researchers observe Möbius strips of polarization having 3/2 or 5/2 twists. These strips demonstrate the rich structure that a light beam can possess at very small, subwavelength distance scales, Boyd explained. He added that, moreover, the measurement technique used here holds great promise for probing the nanostructure of other sorts of light beams.
More information: Observation of optical polarization Möbius strips, Science, www.sciencemag.org/content/ear … nce.1260635.abstract
Journal information: Science
Provided by University of Rochester