December 15, 2014 feature
'Fibonacci quasiparticle' could form basis of future quantum computers
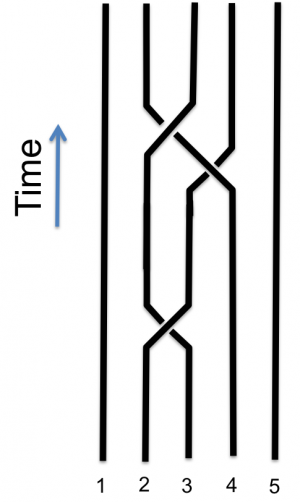
(Phys.org)—Topological quantum computing (TQC) is a newer type of quantum computing that uses "braids" of particle tracks, rather than actual particles such as ions and electrons, as the qubits to implement computations. Using braids has one important advantage: it makes TQCs practically immune to the small perturbations in the environment that cause decoherence in particle-based qubits and often lead to high error rates.
Ever since TQC was first proposed in 1997, experimentally realizing the appropriate braids has been extremely difficult. For one thing, the braids are formed not by the trajectories of ordinary particles, but by the trajectories of exotic quasiparticles (particle-like excitations) called anyons. Also, movements of the anyons must be non-Abelian, a property similar to the non-commutative property in which changing the order of the anyons' movements changes their final tracks. In most proposals of TQC so far, the non-Abelian statistics of the anyons has not been powerful enough, even in theory, for universal TQC.
Now in a new study published in Physical Review Letters, physicists Abolhassan Vaezi at Cornell University and Maissam Barkeshli at Microsoft's research lab Station Q have theoretically shown that anyons tunneling in a double-layer system can transition to an exotic non-Abelian state that contains "Fibonacci" anyons that are powerful enough for universal TQC.
"Our work suggests that some existing experimental setups are rich enough to yield a phase capable of performing 'universal' TQC, i.e., all of the required logical gates for the performance of a quantum computer can be made through the braiding of anyons only," Vaezi told Phys.org. "Since braiding is a topological operation and does not perturb the low-energy physics, the resulting quantum computer is fault-tolerant."
The physicists' work builds on previous research that has shown that anyons can arise due to the fractional quantum Hall effect. To realize this effect, a 2-D electron gas is sandwiched between two flat semiconductor plates. When cooled to temperatures near absolute zero and exposed to strong magnetic fields, excitations form in the 2-D electron gas and give rise to anyons. So far, only Abelian anyons have been detected in fractional quantum Hall systems, but studies suggest that non-Abelian anyons might also be realized.
In the new study, the scientists considered a double-layer fractional quantum Hall system in which anyons can tunnel between the two layers. When modeling this system on a torus, the scientists showed that sufficiently large tunneling drives the evolution of six ground states that correspond to six topologically distinct types of quasiparticles, one of which is the Fibonacci anyon.
Vaezi explains that the Fibonacci anyon is related to the famous Fibonacci sequence (where a number in the sequence is the sum of the previous two numbers) as well as the golden ratio, 1.617… (which is approximately the ratio of any number in the Fibonacci sequence to the previous number). These mathematical patterns arise in the Fibonacci anyon because of its quantum properties, particularly those related to the so-called fusion rules that govern particle spins.
"The Fibonacci anyon is a non-Abelian anyon whose quantum dimension is the golden ratio (1.617...), and is the simplest anyon capable of performing universal quantum computation," Vaezi explained. "Using the fusion rule of Fibonacci anyons, it can be shown that the degeneracy of the ground state in the presence of n well-separated Fibonacci anyons on a sphere is the nth number in the Fibonacci sequence."
So what makes the Fibonacci anyon so attractive for TQC? The answer lies in its braiding statistics, or the way that these quasiparticles move around each other, creating braids and knots of tracks. Three or four Fibonacci anyons may correspond to a single qubit, and their braiding statistics corresponds to single-qubit gates. Building multiple-qubit gates requires braiding multiple qubits, often in intricate ways.
Here the physicists explain that another way to view this process is by looking at quasiparticles as domain walls that separate different ground state patterns of electrons. Different quasiparticles have different electric charges, so they separate different electron patterns. From this perspective, the Fibonacci anyon is appealing due to the particular ground state patterns it separates.
The physicists show that their finding that interlayer tunneling can result in Fibonacci anyons is well-supported by a variety of distinct methods. Further, the researchers raise the possibility that these Fibonacci anyons may have already been realized in past experiments on double-layer quantum Hall systems, although these experiments were not specifically looking for them. This is one area that they hope to investigate in the future.
"To test our prediction, we are numerically studying bilayer quantum Hall states with a number of interlayer interactions and searching for non-Abelian phases and, in particular, Fibonacci anyons in the case of the 2/3 state," Vaezi said. "We are also working on various experimental aspects of our proposal and potential signatures of the Fibonacci anyons."
More information:
Abolhassan Vaezi and Maissam Barkeshli. "Fibonacci Anyons From Abelian Bilayer Quantum Hall States." Physical Review Letters. DOI: 10.1103/PhysRevLett.113.236804
arXiv:1403.3383 [cond-mat.str-el]
Corrected: 3:30pm EST, 12/15/2014: Thanks to El_Nose.
Journal information: Physical Review Letters
© 2014 Phys.org