November 26, 2014 feature
Beyond geometry: Shape entropy links nanostructures with emergent macroscopic behavior in natural and engineered systems
(Phys.org) —Shape has a pervasive but often overlooked impact on how natural systems are ordered. At the same time, entropy (the probabilistic measure of the degree of energy delocalization in a system) – while often misunderstood as the state of a system's disorder – and emergence (the sometimes controversial observance of macroscopic behaviors not seen in isolated systems of a few constituents) are two areas of research that have long received, and are likely to continue receiving, significant scientific attention. Now, materials science and chemical engineering researchers working with computer simulations of colloidal suspensions of hard nanoparticles at University of Michigan, Ann Arbor have linked entropy and emergence through a little-understood property they refer to as shape entropy – an emergent, entropic effect – unrelated to geometric entropy or topological entropy – that differs from and competes with intrinsic shape properties that arise from both the shape geometry and the material itself and affect surface, chemical and other intrinsic properties.
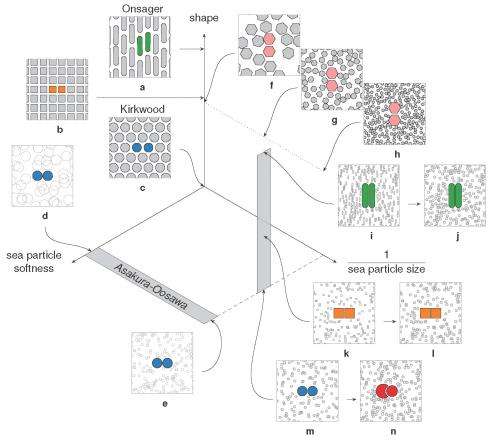
According to the researchers, shape entropy directly affects system structure through directional entropic forces (DEFs) that align neighboring particles and thereby optimize local packing density. Interestingly, the scientists demonstrate that shape entropy drives the emergence of DEFs in a wide class of soft matter systems as particles adopt local dense packing configurations when crowded and drives the phase behavior of systems of anisotropic shapes into complex crystals, liquid crystals and even ordered but non-periodic structures called quasicrystals through these DEFs. (Anisotropy refers to a difference in a material's physical or mechanical properties – absorbance, refractive index, conductivity, tensile strength, and so on – when measured along different axes.)
Prof. Sharon C. Glotzer discussed the paper that she, lead author and Research Investigator Dr. Greg van Anders and their co-authors published in Proceedings of the National Academy of Sciences, noting that one of the fundamental issues they faced was the historical problem of linking microscopic mechanisms with macroscopic emergent behavior. "This is a difficult problem that was really, to our knowledge, only brought into sharp contrast for physical systems by Philip Warren Anderson in his 1972 essay More is Different1 – and really, the title says it all," van Anders tells Phys.org. (Anderson is a physicist and Nobel laureate who in his essay addressed emergent phenomena and the limitations of reductionism.) "We're interested in the type of systems that are dominated by entropy – meaning that their behavior originates from effects of the system as whole," Glotzer points out. "In a way, we're grappling with the problem of how things that operate with basic rules can produce complicated behavior." For Glotzer and her team, the rules are shapes, and the behavior takes the form of complex crystals. "It's very important to understand shape effects in nanosystems," she adds, "because nanoparticles tend to have a natural shape to them because of how they grow."
In addressing this problem, the scientists – in addition to isolating shape entropy in model systems – had to precisely delineate between and correlate the relative influences of shape entropy and intrinsic shape effects. This can be formidable: While the intrinsic shape of a cell or nanoparticle affects a range of other intrinsic properties, such as its surface and chemical characteristics, shape entropy is an effect that emerges from the geometry of the shape itself in the context of other shapes crowded around it. "Intrinsic shape effects are conceptually straightforward because they're forces that originate from van der Waals, Coulomb, and other electrostatic and other forces, though in practice they may not be easy to measure experimentally," Glotzer explains. "However, comparing intrinsic shape effects to shape entropy is a bit like comparing apples and oranges: there are many ways to characterize shapes, but forces aren't typically one of them." Moreover, research has historically focused on shape effects in specific systems, so a general solution was elusive, and there were no rules specifying the types of systems where shape effects might be seen.
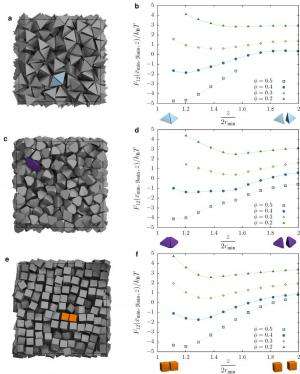
Not surprisingly, then, a significant obstacle was quantitatively demonstrating that shape drives the phase behavior of systems of anisotropic particles upon crowding through directional entropic forces. "Our main problem here was trying to understand how there could be a local mechanism for global ordering that acts through entropy – which is a global construct," Glotzer says. "It took us a while to realize that other investigators had already been asking this question for systems containing mixtures of large particles and very small particles." (The latter, known as depletants, induce assembly or crystallization of larger particles.) "However," she continues, "it was more challenging to determine how to pose and interpret this question mathematically when all particles are the same." Glotzer adds that the technique van Anders and the rest of her team used to understand these systems – the potential of mean force and torque (PMFT), a treatment of isotropic entropic forces first given in 1949 by Jan de Boer2 at the Institute for Theoretical Physics, University of Amsterdam – is in many ways rather basic. Nevertheless, and somewhat remarkably, PMFT provided them with the key by allowing them to quantify directional entropic forces between anisotropic particles at arbitrary density. (PMFT is related to the potential of mean force, or PMF, an earlier approach that - unlike PMFT - has no concept of relative orientation between particles, and regarding shapes would only provide insight into radial, but not angular, dependence.)
The paper also address the relationships between shape entropy, self-assembly and packing behavior. (Self-assembly refers to thermodynamically stable or metastable phases that arise from systems maximizing their generalized entropy through spontaneous self-assembly in the presence of energetic and volumetric constraints, such as temperature and pressure; or through directed self-assembly due to other constraints, such as electromagnetic fields.) "Once we had determined how to measure the directional entropic forces," van Anders explains, "the entropy/self-assembly connection became evident: On the systems we studied, the forces we were able to measure between particles were exactly in the range they should be to contribute to self-assembly (several kBT), which is on the order of intrinsic interactions between nanoparticles and on the scale of temperature-induced random motion." (The metric kBT is the product of the Boltzmann constant, k, and the temperature, T, used in physics as a scaling factor for energy values or as a unit of energy in molecular-scale systems.)
That said, the scientists were able to use directional entropic forces to draw a distinction between self-assembly and packing behavior. "This was puzzling: For a long time, global density packing arguments have been used to predict assembly behavior in a range of systems," Glotzer continues. "However, in the last few years – especially as researchers began looking more seriously at the anisotropic shapes being fabricated in the lab – these packing arguments started failing. Around the same time my group wrote a paper that showed that the assembled behavior can often be predicted by looking at the structure of a dense fluid of particles that hasn't yet assembled." The researchers realized that the forces they were seeing in their calculations were coming from local dense packing that happens in the fluid and the assembled systems. This showed that self-assembly and packing behavior were related, but not by global dense packing.
An important implication of understanding how shape entropy drives both self-assembly and packing despite their observable differences, Glotzer points out, is that there is growing interest in making ordered materials for various optical, electronic and other applications. "We've shown that, in general, it's possible to use shape to control the structure of these materials," she explains. "Now that we understand why particles are doing what they do when they form these materials, it becomes much easier to determine how to design them to generate desired materials rather than just going by trial-and-error."
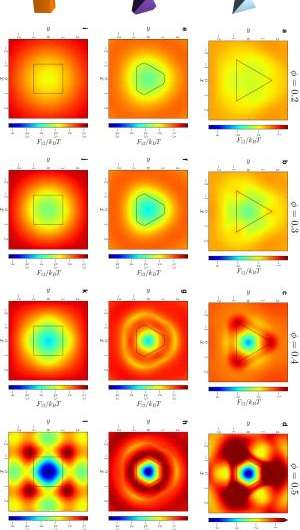
Another dramatic realization was that shape entropy drives the phase behavior of systems of anisotropic shapes through directional entropic forces. "We already knew from prior work in my group that you can quite often predict what crystal structure will form by looking at the fluid and the particle shape," Glotzer tells Phys.org. "The problem for us was identifying what caused particles to arrange into the local structures they did in the fluid, and to show that they had the same sort of structure when they assembled." Van Anders adds that the scientists were able to find the forces that induced and kept the particles in their preferred structures. "When they turned out to be in the right range we knew that we had it right."
To date, the researchers have conducted their simulation studies only on idealized model systems. "Still," says Glotzer, "our simulations capture what we believe to be the most important features of real colloidal systems." Indeed, a growing number of published experimental studies now report the same structures her team predicted, and no counter-results have yet been observed. "We're working closely with collaborators to leverage existing experimental techniques that will allow us to measure the strength of these forces and compare them with our predictions." One such approach is measuring directional entropic forces in the lab by using confocal microscopy to determine the location and orientation of particles in assembling systems.
Moreover, Glotzer's research group is collaborating with several experimental groups to investigate potential approaches to exploiting shape effects in the laboratory. "Now that we understand how local entropic forces work," she tells Phys.org, "we can begin to think about designing particles so that entropy and internal energy balance in just the right way to yield complex target structures."
Glotzer and van Anders conclude that "Researchers have been thinking about different kinds of entropy-driven systems since the 1930s, and since the 1950s have done a lot of work in systems in so-called depletant mixtures – but to our knowledge most people tend to think of those systems as having little to do with densely crowded, single-particle systems. Our work helps to tie these different lines of research together – and we hope that the decades of work done by the community in trying to understand depletant systems can help us get a deeper understanding of pure, dense systems, so that we can narrow our search for interesting new materials."
More information: Understanding shape entropy through local dense packing, Proceedings of the National Academy of Sciences (2014) 111(45):E4812-E4821, doi:10.1073/pnas.1418159111
Related:
1More is Different, Science (1972) 177(4047):393–396, doi:10.1126/science.177.4047.393 (PDF)
2Molecular distribution and equation of state of gases, Reports on Progress in Physics (1949) 12(1):305–374, doi:10.1088/0034-4885/12/1/314
Journal information: Proceedings of the National Academy of Sciences , Science , Reports on Progress in Physics
© 2014 Phys.org