September 29, 2014 feature
Now hear this: Simple fluid waveguide performs spectral analysis in a manner similar to the cochlea
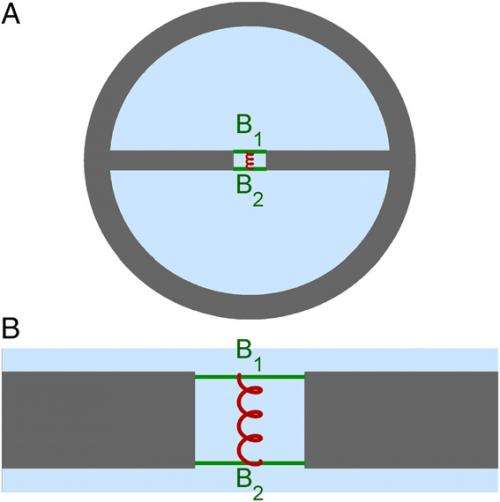
(Phys.org) —Within the mammalian inner ear, or cochlea, a remarkable but and long-debated phenomenon occurs: As they move from the base of the cochlea to its apex, traveling fluid waves – that is, surface waves, in which (like waves on the sea and or in a canal) water moves both longitudinally and transversally – peak in amplitude at locations that depend on the wave's frequency. (Higher frequencies are concentrated in the base, lower frequencies in the apex.) What's critical is that these peaks allow us to identify and separate sounds. While cochlear frequency selectivity is typically explained by local resonances, this idea has two problems: resonance-based models require excessive intracochlear mass, and moreover cannot accurately represent the cochlea's production of both phase and amplitude information. Recently, however, Prof. Marcel van der Heijden at Erasmus Medical Center, University Medical Center, Rotterdam, has rejected resonance, and in its place has designed and fabricated a novel neural data-inspired approach to producing these frequency-dependent amplitude peaks in the form of a disarmingly simple waveguide that, in a manner analogous to an optical prism, carries fluid waves and performs spectral analysis. By incorporating a longitudinal gradient, the waveguide – which consists of two parallel fluid-filled chambers connected by a narrow slit spanned by two coupled elastic beams – separates frequencies and decelerates energy transport through wave dispersion, thereby focusing the peak-creating energy. Its novelty derives from its spectral analysis functionality being based not on resonance, nor on standing waves or geometric periodicity, but on mode shape swapping – an abrupt exchange of shapes between propagating wave modes – making it a new physical effect based on well-known physics.
Remarkably, although van der Heijden intentionally eschewed the creation of a complex biophysical model, the waveguide nonetheless displays strong structural and behavioral similarities to the cochlea. That said, the paper acknowledges that the current model cannot describe the multiband dynamic range compression performed by the living cochlea, which would require automatic gain control or the ability to direct high-intensity waves into the nonpeaking mode. To that end, the paper also states that "refinement of optical coherence tomography techniques will undoubtedly deepen the knowledge of inner ear vibrations in unprecedented ways," and that the study's findings provide a "clear and straightforward theoretic framework that can guide the interpretation of such data." Optical coherence tomography (OCT) is an optical signal acquisition and processing method that captures micrometer-resolution, three-dimensional cross-sectional images from within biological tissue and other optical scattering media in situ and in real time. OCT is analogous to ultrasound imaging, but employs light (typically near-infrared) rather than sound.
Prof. van der Heijden discussed the paper that he published in Proceedings of the National Academy of Sciences with Phys.org, noting that he faced one major challenge in designing and fabricating the simplest possible fluid waveguide that exhibits steep deceleration and peaking: determining the precise physics behind the steep wave deceleration. "Consider the peaking by imagining a duct that, like a canal, mediates water waves – but with an important difference: the waves in this system first travel some distance and then suddenly grow in amplitude, peak, and decay rapidly – and even more interestingly, the location of the peak depends on the frequency of the wave," van der Heijden tells Phys.org, with low-frequency waves travelling farther before they peak. This strange system exists: our own inner ears and those of other mammals host these peaking waves, and that is how they perform a spectral analysis of sound." The challenge – and opportunity – is that scientists still don't understand the underlying physics due primarily to a lack of data. There's a good reason for this: The inner ear is not amenable to experiment, as it is inaccessible and vulnerable, with the vibrations in the nanometer range.
"Current dogma in inner-ear mechanics states that the peaking is caused by a form of biological amplification that injects mechanical energy into the sound-evoked wave," van der Heijden continues, "but I'm skeptical about the existence of what is customarily termed a cochlear amplifier." His position makes sense, since after 35 years the evidence for amplification is still circumstantial at best, and experts disagree on the basic mechanisms. "Amplification requires phase-locked mechanical feedback to high-frequency input – as high as 100 kHz for bats and dolphins – which is physiologically very implausible." Moreover, he points out, it serves no known purpose: In order to amplify faint sounds, you need to detect them in the first place – so why not stop there if your aim is to hear the sound? "You might think that amplifying faint signals improves their detectability, but that is not the case. Amplifiers always worsen the signal-to-noise ratio."
An alternative to amplification – the one that van der Heijden has taken – is focusing available sound energy. "In a wave this is done by slowing it down, which causes a traffic jam-like congestion of the energy. In addition, from measurements we know that by the time the vibrations are converted to neural signals, the speed of the energy transport has slowed down to a mere walking pace. No amplifier needed!" In fact, in vivo experiments1 by van der Heijden and his former PhD student Corstiaen Versteegh showed that deceleration is steep, giving sharp peaking. "However," van der Heijden emphasizes, the question now becomes, What is the physics behind the steep wave deceleration?" In the paper, van der Heijden notes that he expects that these new data and ideas will help them to understand the basis of cochlear frequency selectivity and gain control in the near future.
Another aspect of his study is determining precisely how the waveguide acts to spatially separate the frequency components of a wideband input. "Once you know how to build a waveguide that shows steep deceleration for one frequency, you can turn it into a spectral analyzer by introducing a longitudinal gradient. In this graded system, every frequency component travels fast until it reaches its own region of steep deceleration, at which will its amplitude will be magnified. The subsequent decay comes from the fact that slowly propagating waves are more susceptible to damping." It is important to note that in this graded system, every frequency component delivers its energy at its proper place, making it a spectral analyzer. "Therefore," he adds, "the main challenge is to design a waveguide in which frequencies up to, say, 1000 Hz travel fast, and all frequencies above 1000 Hz travel much more slowly. If you can do that, the rest is just details."
As might be expected, van der Heijden says that his key insight was the rejection of resonance – a well-accepted but nevertheless flawed attempt to model the inner ear put forth by Hermann von Helmholtz in the 1850s. More recently, in 1980 James Lighthill analyzed the combination of resonance with traveling waves. "An authority on fluid dynamics, Lighthill found that this combination creates deceleration and peaking," van der Heijden explains. "While this appears useful, he also showed that such waves never get beyond their matching resonator – that is, they slow down indefinitely before reaching it. At the same time, our experimental data clearly showed a steep deceleration, but never a complete standstill – meaning that the wave shifts gears, but does not stop. Exit resonance."
Van der Heijden's second insight came from studying fluid waves, which he charmingly describes as a delightful 19th-century physics topic. "Waves in shallow water are simple, in that all frequencies travel equally fast. However, in deep water there's dispersion, with high frequencies propagating more slowly than low frequencies – and modifying the geometry strengthens dispersion. Imagine a deep lake covered with a layer of ice. Now cut a long, narrow slit in the ice, exposing the water," he illustrates. "When you disturb the water, the waves propagating along the slit show an extreme form of dispersion. While this geometry resembles that of the cochlear fluid-filled canals, or scalae, van der Heijden points out that the dispersion obtained in this way is still too gradual to fully explain the steep deceleration of the waves observed in the cochlea.
Interestingly, his third insight came from quantum mechanics, where bound systems have discrete energy levels. "When gradually changing the system – for instance, by applying a variable magnetic field – some energy levels may shift more than others, suggesting that you might be able to get two levels to cross by one overtaking the other," van der Heijden tells Phys.org. "However, this does not happen: Instead, the two energy curves veer away sharply where they should cross, each following the projected trajectory of the other in what is known as avoided crossing. Von Neumann and Wigner articulated the mathematical explanation in 1929, and since wave propagation in complex systems is described by the same mathematical formalism, this suggests that avoided crossing can also occur in waves." Indeed, he recounts, taking a waveguide that supports both deep and shallow waves, and manipulating only the shallow waves by installing an extra spring, he created a situation in which the dispersion curves of the shallow and deep waves were set to cross – but didn't. "The avoided crossing produces a sharp kink in both curves, and this kink corresponds to the steep deceleration in one of the modes," he explains. "Physically, the two modes exchange shape, meaning that mode shape swapping induces the sudden change of the speed of energy transport."

The paper predicts that in the near future the waveguide model and mode shape swapping will enhance understanding of cochlear frequency selectivity and gain control. "In terms of frequency selectivity, I say this because despite the math, the waveguide itself is almost embarrassingly simple compared to typical cochlear models based on resonance and amplification, and comprises only passive, linear elements," van der Heijden notes. In other words, since its behavior depends on so few parameters, there is little opportunity to tweak the system, so it thereby makes a very specific prediction – namely, that the internal vibration mode of the cochlea changes drastically when varying the sound frequency. "The model therefore provides a clear theoretical framework to guide experiments," he adds, "and recent developments in imaging techniques2 will enable testing these predictions. Should they be confirmed, this amounts to a huge simplification of the mechanisms behind auditory tuning… basically, some water and a handful of springs and dashpots" – dampers that resist motion via viscous friction – "instead of complicated feedback loops, amplifiers and resonators."
As for gain control, van der Heijden points out that our ears mechanically compress the dynamic range of sounds, and that this is done more or less independently in different frequency bands. "Current models implement gain control by a saturation of the amplifier elements. In the mammalian ear, this role is played by outer hair cells, which act both as sensors and actuators. My waveguide model is linear, so it has no gain control – yet: When local vibrations become too large, a simple array of what can be thought of as automatic brakes will engage, with a given brake damping the waves that peak near it. Again, while outer hair cells are also suited, braking is much simpler than amplifying!" Specifically, amplification requires extreme temporal acuity and braking does not – so again, the model leads to a significant simplification of the mechanisms and, again, calls for specific experiments, such as measuring the temporal acuity of the gain control in actual ears.
One of the wider implications of spectral analysis though propagating wave mode shape exchange is that the modest structural requirements for mode shape swapping to occur in a fluid waveguide suggest its possible role in the spectral analysis by non-mammalian ears, such as birds, reptiles and amphibians. "These ears show a much larger morphological variety than the mammalian cochlea," van der Heijden says. "Furthermore, the generality of the underlying principles of wave modes and dispersion raises the possibility of realizing mode shape swapping in entirely different settings such as optics."
Because spectral analysis and multiband gain control of sounds are already implemented in silico in cochlear implants, van der Heijden sees no particular advantage in replacing them with a mechanical device. "We're currently much better in miniaturizing electronics than in miniaturizing mechanical devices such as outer hair cells, so I think that the electronic gain control of modern cochlear implants is hard to beat – and they may well be superior to the natural gain control of our ears, which isn't that good anyhow. However," he adds, "there's another twist to this story: If I'm right that gain control is a brake rather than an amplifier, it may change our perspective on cochlear hearing loss. This makes it crucial to understand the exact mechanisms and cochlear structures involved in gain control."
Relatedly, van der Heijden notes that the auditory neural pathway interface is the bottleneck of all implants. "Electrical stimulation of the auditory nerve through the cochlear fluid is frustratingly unselective compared to the natural situation, where each of the thousands of nerve fibers targets exactly one inner hair cell," he explains. "Therefore, even if a multi-electrode device has perfect spectral analysis and superior multiband gain control, most of that wealth is lost upon interfacing it to the nerve – which is why most implant users cannot enjoy music and have severe trouble with background noise. Theoretically, it would be better to mechanically stimulate the inner hair cells – if enough are left – but apart from building a multi-actuator micromechanical device, it would be difficult to insert it into the helical cochlear duct without ruining the soft tissues that are crucial to proper inner hair cell function."
Moving forward, van der Heijden and his research team will continue their measurements of nanometer vibrations in living inner ears of lab animals – and, not surprisingly, their focus is on gain control: "How does sound intensity affect wave propagation? When presented with rapid intensity fluctuations, what is the highest rate at which gain control can follow? We know it's rapid, but temporal limits will inform us about the underlying mechanisms."
Regarding the waveguide model, he acknowledges that there are many questions to be answered, including:
- Which parameters determine the tuning sharpness?
- Once that is known, can we interpret the differences in hearing between species in terms of their different cochlear morphology?
- Can the model be adapted to mimic highly specialized cochleae like those of echolocating bats with their sharp filtering in a narrow frequency band?
- How can we incorporate gain control that mimics that of real ears?
- Currently the model is highly stylized. Can it be made more physiological, leading to more detailed predictions on the internal motions of inner-ear structures, which can then be tested experimentally?
Regarding other innovations they might consider developing, van der Heijden says "I'd love to collaborate with experimental hydrodynamic experts and see if we can build a large-scale version of the fluid waveguide. It's one thing to solve equations and describe an effect; it's another to actually make it work in reality." If successful, this could also provide insight into the critical structural properties of the inner ear.
A number of other areas of research might benefit from their study, including, radio astronomy, precision sonar, and tissue analysis. "In principle, mode shape swapping could occur for any type of dispersive waves," van der Heijden tells Phys.org. "The steep nature of the transition suggests its application to situations where a sensitive control of wave propagation is desired. In particular, optical realizations could be useful for filtering, switching or beam separation, while spectral analysis based on mode shape swapping may be useful in cases where other methods are unfeasible or have undesired side effects. Ideally," he concludes, "reading the paper would help someone from another area to solve a problem I have never heard of!"
More information: Frequency selectivity without resonance in a fluid waveguide, Proceedings of the National Academy of Sciences Published online before print September 18, 2014, doi:10.1073/pnas.1412412111
Related:
1The Spatial Buildup of Compression and Suppression in the Mammalian Cochlea, Journal of the Association for Research in Otolaryngology August 2013, Volume 14, Issue 4, pp 523-545, doi:10.1007/s10162-013-0393-0
2Vibration of the organ of Corti within the cochlear apex in mice, Journal of Neurophysiology 1 September 2014, Vol. 112 no. 5, 1192-1204, doi:10.1152/jn.00306.2014
© 2014 Phys.org