Can maths cure cancer?
Scientists, including Professor Tanniemola Liverpool from the University of Bristol's School of Mathematics, claim that by understanding how an artificial 'synthetic swimmer' can be made and driven, and how such swimmers behave in large groups as 'soft active matter', is the answer to developing new improved drug control to cure cancer. The payoff would be the ability to target the specific affected cancerous area, rather than the entire body as in the current chemotherapy approach.
To imagine this idea, physically consider the following: Bob falls over and grazes his knee and within a few minutes his white blood cells have accumulated at the grazed area and a scab forms. To create a 'swimmer' that can behave like these white blood cells one needs to understand how the white blood cells are driven to the cut on his knee, what speed they travel and how they know in which direction to go.
Many researchers are currently designing such self-driven swimmers that can be driven to a specific target area, just like these white blood cells. These swimmers would act as the key tool to control drug doses in specific target areas of a body. Professor Liverpool has developed mathematical models and theories to explain the behaviour of such swimmers. To date, his calculations provide a guide for optimizing the design of swimmers for any given available surface properties, in which (for example) the velocity can be controlled.
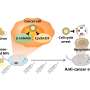
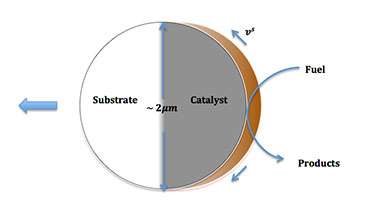
The figure (above), drawn by Professor Liverpool's PhD student Yahaya Ibrahim, represents such a swimmer. It consists of a polystyrene bead, half coated with a platinum catalyst. A catalyst is a substance that speeds up a reaction. In this case the platinum catalyses the process of hydrogen dioxide to oxygen and hydrogen. When the bead is placed into water, the increased chemical reaction on one side of the bead creates a hydrodynamic flow around the object. This hydrodynamic flow then makes the swimmer move. A system has been created that 'drives' the bead, making the bead seem active and alive, like the white blood cell.
Professor Liverpool predicts the dynamics of this by modelling and combining the chemistry and the mathematical and electrostatic properties of the swimmer.
The theory does not stop with describing the dynamics for just one swimmer. Predicting behaviour of large groups of swimmers is just as important. Blood, for example is not made up of one but many white blood cells. Professor Liverpool's work in this area has provoked a new set of questions and open problems for experimentalists to consider.
Experimental work has been instrumental in providing data that helps inform and expand the scientific model for a larger family of swimmers. For example, for the 'polystyrene bead' swimmer, both the electrostatic effects and hydrodynamic effects that result from the reaction affect the flow field around the object. It is this flow field that then affects the direction that the swimmer will move. Being able to direct a swimmer to a certain area is crucial when it comes to designing the improved cancer drug treatment. Varying reactions with other catalysis or substances generate different ratios of electrostatic and hydrodynamic effects. This in turn changes the flow field, which changes the direction the swimmer will travel. Currently these ratios are not clear, but are essential to control the direction of a swimmer. Once more is known on how these ratios can vary for different reactions, this information can be implanted to improve the model for swimmers in different environments.
Although a lot is now understood about synthetic swimmers, both alone and in large groups, many new open questions are being raised. This makes the topic a very active area of research that lies at the crossroads of physics, chemistry, biology and, fundamentally, mathematics!
Provided by University of Bristol