February 26, 2014 feature
Fusion, and friction, and fields! Oh, my! The rich and ubiquitous world of fluid dynamics
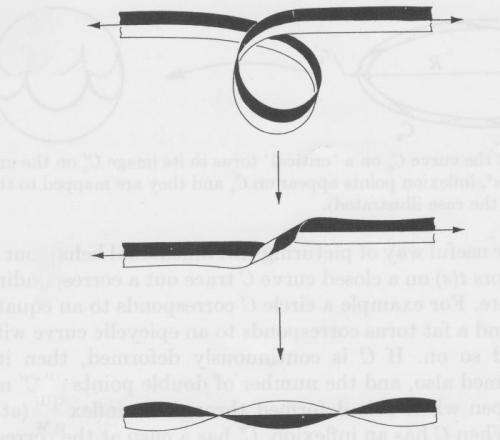
Fluid dynamics – a subset of the area of physics known as fluid mechanics – is concerned with the motion, or flow, of liquids and gases. Within fluid dynamics, a vortex is a region within a fluid where the flow is essentially a spinning motion about an imaginary straight or curved axis. In this context, helicity represents the degree of linkage of the flow's vortex lines, conserved when these are frozen in the fluid.
Fluid dynamics has wide utility, with applications as diverse as human physiology (physiological fluid dynamics), the flight of insects, birds and aircraft (aerodynamics), the recovery of oil through porous media, the dynamics of ocean and atmosphere (geophysical fluid dynamics), the design of future fusion reactors (plasma dynamics and magnetohydrodynamics), and the understanding of astrophysical processes in stars and galaxies (astrophysical fluid dynamics). Recently, Prof. H. Keith Moffatt – an applied mathematician at the University of Cambridge, UK, with decades of seminal contributions in the field of fluid dynamics – published a paper reviewing several properties of helicity, including cosmological magnetic fields, topological flows, turbulence energy cascades, fusion reactor magnetic field configuration.
Prof. Moffatt discussed the paper he published in Proceedings of the National Academy of Sciences with Phys.org, beginning with the main challenges to determining the role of helicity in the areas he reviewed. "Helicity in a turbulent flow of a conducting fluid usually arises from a combination of convection and Coriolis effects," Moffatt tells Phys.org. (In physics, the Coriolis effect is a deflection of moving objects when viewed in a rotating reference frame. "These processes, acting in conjunction, can break the so-called reflectional symmetry of turbulence statistics – and helicity is a measure of the resulting lack of reflectional symmetry. Moreover," he continues, "it's now firmly established that under these circumstances, a magnetic field will grow spontaneously on a scale that can be much larger than the scale of the underlying turbulence – an example of what is referred to as order out of chaos." The magnetic fields of stars and planets are generated ordinarily by this process, as are the time-dependent evolution of these fields – for example, random reversals of the Earth's magnetic polarity. "This dynamo excitation of magnetic fields in cosmic systems," Moffatt adds, "continues to pose major challenges for theoreticians."
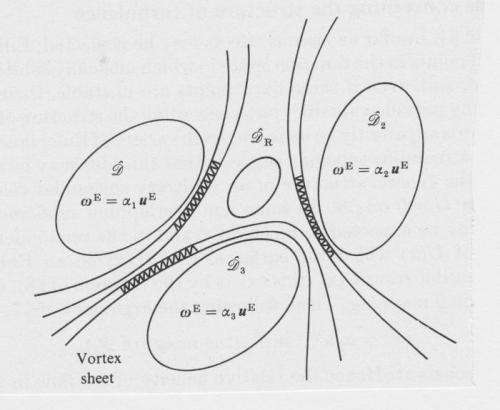
Another challenge, he points out, is determining the role of helicity in so-called Euler flows of arbitrarily complex streamline topology. "There's an exact analogy between steady Euler flows of an ideal incompressible fluid and magnetostatic equilibria in a perfectly conducting medium." (In fluid dynamics, the Euler equations govern inviscid, or zero viscosity, flow – and assuming an ideal incompressible flow simplifies the resulting flow equations.) "The latter may be determined by a relaxation procedure dependent on the invariance of magnetic helicity, and are stable within the limits of the perfect conductivity assumption. The analogy can then be exploited to demonstrate the existence of Euler flows of arbitrary topological complexity. Unfortunately the analogy does not extend to stability considerations, and such flows are in fact almost invariably unstable due to the presence within them of vortex sheets which are subject to the classical Kelvin-Helmholtz instability."
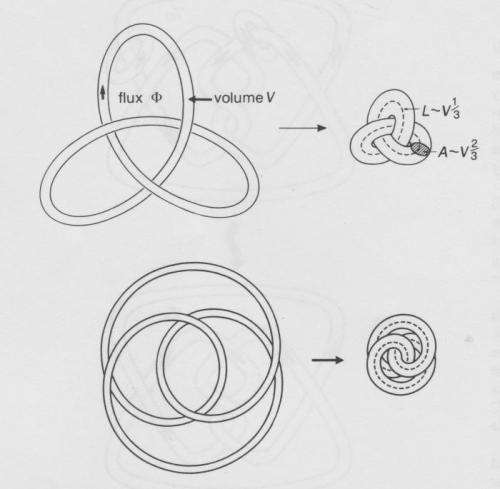
Another issue is the determination of stable knotted minimum-energy magnetostatic structures. (Knots and links play a fundamental role in a wide range of fields, including quantum and classical plasmas and fluids. In fluids, the fundamental knottedness-carrying excitations occur in the form of linked and knotted vortex loops.) "Stable knotted minimum energy structures can in principle be determined by the above relaxation procedure," Moffatt says. "These are knotted magnetic flux tubes, within which the field lines may be twisted into helical form, this contributing to the overall helicity of the structure. The challenge here is to determine the minimum magnetic energy function m(h) for any given knot K, and to thereby establish a bridge with the purely geometric theory of so-called tight knots."
A critical aspect of fluid dynamics is turbulence and, in relation to helicity, what's known as depleting nonlinearity in the Navier-Stokes equations that describe the motion of fluid substances.) More specifically, the nonlinearity of the Navier-Stokes equations arises from transport of the vorticity, or spin vector, of the fluid by the associated velocity field. This nonlinearity is minimized in any region where vorticity and velocity are parallel – which happens to be precisely those regions where helicity magnitude is maximized. "It's therefore reasonable," Moffatt notes, "to conjecture that helicity has a significant influence on the nonlinearity that is responsible for the transfer of energy from large to ever-smaller scales at which viscosity, however weak, ultimately can dissipate the turbulent energy."
When it came to addressing these challenges, Moffatt's first insight was recognizing that helicity is a measure of the degree of knottedness and/or linkage of the vortex lines of the flow. "This established a bridge between classical fluid mechanics and topology," he explains. "This insight, coupled with the technique of magnetic relaxation, led to the idea that one could unambiguously associate an energy spectrum with any knotted or linked structure. In the context of dynamo theory, recognition of helicity as a key property of turbulence provided a firm foundation for kinematic theory, and opened the door to a more ambitious fully dynamic theory of dynamo action, with saturation of the exponential growth provided by suppression of helicity by the growing magnetic field." Kinematics – often referred to as the geometry of motion – is the branch of classical mechanics which describes the motion of points, objects and groups of objects without considering the causes of that motion.
In his paper, Moffatt describes how slow viscous flows have relevance for a number of applications, one being the design of micro- and nanofluid devices. "Micro-fluid devices operate at very low Reynolds numbers due to the very small scales involved," he explains. (The Reynolds number is a dimensionless quantity used to help predict similar flow patterns in different fluid flows.) "The properties of fluid flow in such devices need to be understood in the interests of design optimization. My theory of flow near any sharp corner, now 50 years old," he notes, "is relevant for such devices, which frequently involve 2- or 3-dimensional flows in corner regions."
Slow viscous flows also increase the understanding of mixing processes in chemical engineering geophysics. "Mixing of fluids is at the heart of chemical engineering processes, in which the promotion of chemical interaction may be desirable," Moffatt tells Phys.org. "For this purpose the contact area of two fluids – assumed to be immiscible, or unable to be mixed or blended – needs to be maximized." Vigorous stirring mechanisms achieve this result, says Moffatt, frequently through the break-up of one of the fluids into small droplets – and at a microscopic level, this involves topological changes that occur despite the opposing effect of surface tension, which tends to reduce the contact area. "My focus," he adds, "has been on the mechanism of such topological change, which occurs at singular points or curves within the flow."
At an atmospheric or oceanic scale, Moffatt continues, the Reynolds number is extremely large, and low Reynolds number results are less relevant. "However," he adds, "chaos in flows, which is identified through the exponential separation of particle paths, is relevant to the spread of pollutants – for example, from oil spills in the ocean or from volcanic eruptions in the atmosphere. The fact that such chaos can occur even for low Reynolds number steady flow in a closed domain is an indication of the universality of this phenomenon."
Moving forward in terms of the next steps in his fluid dynamics research, Moffatt say, "It's hard to predict the future! At present I'm working on a revision of my 1978 monograph on dynamo theory, and am also collaborating with colleagues on a study of topological transitions that can occur for a soap film on a deforming wire frame." The latter, he notes, is a topic related "in spirit" to other situations, such as vortex reconnection, where topological transitions occur.
As might be expected, a range of other applications and areas of research stand to benefit from Moffatt's study. "Fluid mechanics is relevant to natural phenomena on all scales," Moffatt tells Phys.org, "from the scale of the human cell up to the scale of distant galaxies. In particular," he concludes, "my low Reynolds number studies are relevant to the smallest scales, while my studies in magnetohydrodynamics and dynamo theory are relevant in planetary and astrophysical contexts, as well as to thermonuclear fusion devices." The latter includes, Moffatt adds, the International Thermonuclear Experimental Reactor (ITER), the latest generation and largest Tokomak fusion reactor, under construction in Cadarache, France.
More information: Helicity and singular structures in fluid dynamics, Proceedings of the National Academy of Sciences, Published online before print on February 11, 2014, DOI: 10.1073/pnas.1400277111
Journal information: Proceedings of the National Academy of Sciences
© 2014 Phys.org. All rights reserved.