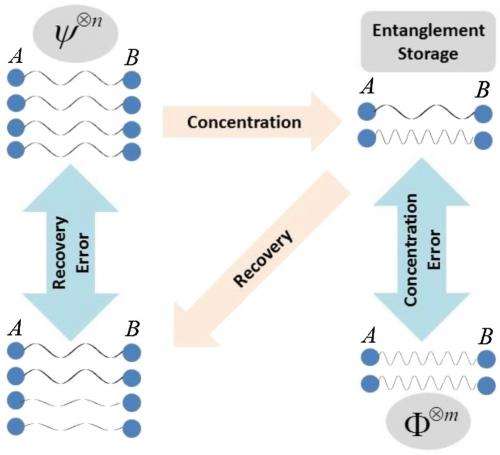
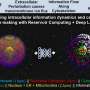
A diagram of entanglement concentration and its recovery operation, entanglement dilution. Scientists have found that an initial entangled state cannot be completely recovered after the concentration process. Credit: Kumagai, et al. ©2013 American Physical Society
(Phys.org) —Several different types of entangled states can be used in quantum information processes, and these states can be converted into one another using a variety of conversion processes. While previous research has suggested that one of the most common types of conversions, called entanglement concentration, is reversible, a new paper shows for the first time that it is irreversible due to a trade-off relation between performance and reversibility. The finding could have implications for future developments in quantum information applications.
The physicists, Wataru Kumagai at Tohoku University in Sendai, Japan, and Nagoya University in Nagoya, Japan; and Masahito Hayashi at Nagoya University and the National University of Singapore, have published their paper on the irreversibility of entanglement concentration in a recent issue of Physical Review Letters.
In quantum information processes, entanglement concentration is used to convert multiple copies of an entangled pure state into multiple copies of an entangled EPR state. Another conversion process, called entanglement dilution, does the opposite; that is, it converts copies of the EPR state into copies of a pure state.
Due in part to the fact that the optimal rates of entanglement concentration and entanglement dilution are the same, physicists have previously thought that entanglement concentration may be reversible. If this were true, reversible entanglement concentration could be used to compress multiple copies of an entangled pure state in a lower dimensional storage system, and later the initial state could be recovered using entanglement dilution.
However, in the current paper the researchers have examined the recovery process more deeply, and have found that it doesn't quite work this way. The physicists explain that the recovery process has two kinds of errors: a concentration error, which represents performance; and a minimum recovery error, which represents the degree of irreversibility.
Complete success occurs when an error is zero, while complete failure occurs when an error is 1. The physicists show that each error can individually attain the value zero, but not at the same time. This happens because of a trade-off between the concentration error and the minimum recovery error. The sum of both errors must always be 1, so that the smaller one error is, the larger the other becomes.
This trade-off implies that, when the concentration error is 0, the minimum recovery error is 1. That is, perfect entanglement concentration is completely irreversible. The researchers describe this irreversibility using an analogy to another type of concentration: concentrated fruit juice.
"The irreversibility of entanglement concentration seems similar to the fact that from-concentrate fruit juice is slightly different from the original juice," Hayashi said, since one process is used to remove water from the juice and another process used to do the opposite. "Commonly, both concentration processes lose a subtle essence from the original."
For practical purposes, this irreversibility means that some of the initial copies of the entangled pure state cannot be recovered from the entangled EPR state. The physicists calculated the minimal concentration-recovery error (MCRE)—which is a combination of both errors—that gives the maximum number of recoverable copies under different circumstances. This formulation could be applied to a variety of quantum information processes.
"Our result shows not only the impossibility of the perfect recovery of the entanglement concentration, but also provides the optimal designs of the entanglement concentration and the recovery operation," Hayashi said. "This design may be used for a better realization of quantum storage of entangled states."
As Hayashi explained, this finding builds on his previous research on irreversibility with respect to data compression.
"Many researchers in the information theory community believed that compressed data up to the Shannon limit is the perfect random number, which is called 'the folklore of source coding," he said. "However, this is not true. In this problem, we considered the decoding error probability of the data compression and the difference of the compressed data from the perfect random number. In 2004, I found the trade-off between the decoding error probability and the difference. Then, I showed that the sum goes to 1 when the size of data goes to infinity."
Although this idea is not well-known in the information community, it inspired the researchers to investigated entanglement concentration irreversibility.
In the future, the researchers plan to use these results to clone entangled states. This cloning is closely related to the irreversibility of entanglement concentration, since the key point of the cloning is the evaluation of error of the recovery operation.
"Now, we consider applying our idea to the cloning of entangled states when a number of copies of a given entangled state are prepared," Hayashi said. "In fact, if we are not allowed to use global quantum operations between distinct parties, i.e., we are allowed to use only local operation and classical communication (LOCC), we cannot increase the amount of entanglement.
"Hence, in this case, even if we know the wave function of the entangled state, we cannot clone the entangled state (i.e., increase the number of copies) without any error. However, if we accept a small size of error, there is a possibility to increase the number of copies. We named this operation the LOCC cloning, which is our current research topic."
More information: Wataru Kumagai and Masahito Hayashi. "Entanglement Concentration is Irreversible." PRL 111, 130407 (2013). DOI: 10.1103/PhysRevLett.111.130407
Journal information: Physical Review Letters
© 2013 Phys.org. All rights reserved.