Getting around the 'uncertainty principle': Physicists make first direct measurements of polarization states of light
Researchers at the University of Rochester and the University of Ottawa have applied a recently developed technique to directly measure for the first time the polarization states of light. Their work both overcomes some important challenges of Heisenberg's famous Uncertainty Principle and also is applicable to qubits, the building blocks of quantum information theory.
They report their results in a paper published this week in Nature Photonics.
The direct measurement technique was first developed in 2011 by scientists at the National Research Council, Canada, to measure the wavefunction – a way of determining the state of a quantum system.
Such direct measurements of the wavefunction had long seemed impossible because of a key tenet of the uncertainty principle – the idea that certain properties of a quantum system could be known only poorly if certain other related properties were known with precision. The ability to make these measurements directly challenges the idea that full understanding of a quantum system could never come from direct observation.
The Rochester/Ottawa researchers, led by Robert Boyd, who has appointments at both universities, measured the polarization states of light - the directions in which the electric and magnetic fields of the light oscillate. Their key result, like that of the team that pioneered direct measurement, is that it is possible to measure key related variables, known as "conjugate" variables, of a quantum particle or state directly. The polarization states of light can be used to encode information, which is why they can be the basis of qubits in quantum information applications.
"The ability to perform direct measurement of the quantum wavefunction has important future implications for quantum information science," explained Boyd, Canada Excellence Research Chair in Quantum Nonlinear Optics at the University of Ottawa and Professor of Optics and Physics at the University of Rochester. "Ongoing work in our group involves applying this technique to other systems, for example, measuring the form of a "mixed" (as opposed to a pure) quantum state."
Previously, a technique called quantum tomography has allowed researchers to measure the information contained in these quantum states, but only indirectly. Quantum tomography requires intensive post-processing of the data, and this is a time-consuming process that is not required in the direct measurement technique. Thus, in principle, the new technique provides the same information as quantum tomography but in significantly less time.
"The key to characterizing any quantum system is gathering information about conjugate variables," said co-author Jonathan Leach, who is now a lecturer at Heriot-Watt University, UK. "The reason it wasn't thought possible to measure two conjugate variables directly was because measuring one would destroy the wavefunction before the other one could be measured."
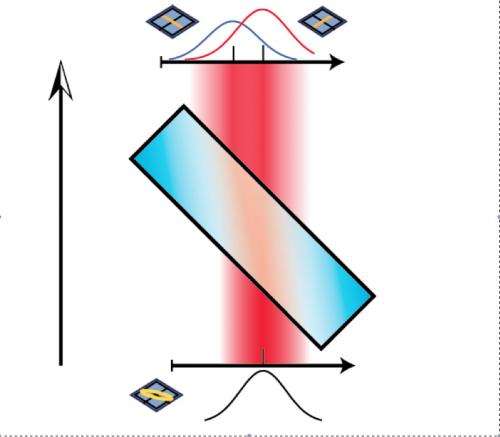
The direct measurement technique employs a "trick" to measure the first property in such a way that the system is not disturbed significantly and information about the second property can still be obtained. This careful measurement relies on the "weak measurement" of the first property followed by a "strong measurement" of the second property.
First described 25 years ago, weak measurement requires that the coupling between the system and what is used to measure it be, as its name suggests, "weak", which means that the system is barely disturbed in the measurement process. The downside of this type of measurement is that a single measurement only provides a small amount of information, and to get an accurate readout, the process has to be repeated multiple times and the average taken.
Boyd and his colleagues used the position and momentum of the light as the indicator of the polarization state. To couple the polarization to the spatial degree of freedom they used birefringent crystals: when light goes through such a crystal, there is a spatial separation introduced for different polarizations. For example, if light is made of a combination of horizontally and vertically polarized component, the positions of the individual components will spread out when it goes through the crystal according to its polarization. The thickness of the crystal can control the strength of the measurement, weak or strong, and determine the degree of separation, correspondingly small or large.
In this experiment, Boyd and his colleagues passed polarized light through two crystals of differing thicknesses: the first, a very thin crystal that "weakly" measures the horizontal and vertical polarization state; the second, a much thicker crystal that "strongly" measures the diagonal and anti-diagonal polarization state. As the first measurement was performed weakly, the system is not significantly disturbed, and therefore, information gained from the second measurement was still valid. This process is repeated several times to build up accurate statistics. Putting all of this together gives a full, direct characterization of the polarization states of the light.
Journal information: Nature Photonics
Provided by University of Rochester