The most distant mature galaxy cluster

Astronomers have used an armada of telescopes on the ground and in space, including the Very Large Telescope at ESO's Paranal Observatory in Chile to discover and measure the distance to the most remote mature cluster of galaxies yet found. Although this cluster is seen when the Universe was less than one quarter of its current age it looks surprisingly similar to galaxy clusters in the current Universe.

"We have measured the distance to the most distant mature cluster of galaxies ever found", says the lead author of the study in which the observations from ESO's VLT have been used, Raphael Gobat (CEA, Paris). "The surprising thing is that when we look closely at this galaxy cluster it doesn't look young -- many of the galaxies have settled down and don't resemble the usual star-forming galaxies seen in the early Universe."

Clusters of galaxies are the largest structures in the Universe that are held together by gravity. Astronomers expect these clusters to grow through time and hence that massive clusters would be rare in the early Universe. Although even more distant clusters have been seen, they appear to be young clusters in the process of formation and are not settled mature systems.

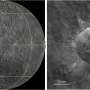
The international team of astronomers used the powerful VIMOS and FORS2 instruments on ESO's Very Large Telescope (VLT) to measure the distances to some of the blobs in a curious patch of very faint red objects first observed with the Spitzer space telescope. This grouping, named CL J1449+0856, had all the hallmarks of being a very remote cluster of galaxies. The results showed that we are indeed seeing a galaxy cluster as it was when the Universe was about three billion years old -- less than one quarter of its current age.

Once the team knew the distance to this very rare object they looked carefully at the component galaxies using both the NASA/ESA Hubble Space Telescope and ground-based telescopes, including the VLT. They found evidence suggesting that most of the galaxies in the cluster were not forming stars, but were composed of stars that were already about one billion years old. This makes the cluster a mature object, similar in mass to the Virgo Cluster, the nearest rich galaxy cluster to the Milky Way.

Further evidence that this is a mature cluster comes from observations of X-rays coming from CL J1449+0856 made with ESA's XMM-Newton space observatory. The cluster is giving off X-rays that must be coming from a very hot cloud of tenuous gas filling the space between the galaxies and concentrated towards the centre of the cluster. This is another sign of a mature galaxy cluster, held firmly together by its own gravity, as very young clusters have not had time to trap hot gas in this way.

As Gobat concludes: "These new results support the idea that mature clusters existed when the Universe was less than one quarter of its current age. Such clusters are expected to be very rare according to current theory, and we have been very lucky to spot one. But if further observations find many more then this may mean that our understanding of the early Universe needs to be revised."