May 7, 2009 feature
Post-Quantum Correlations: Exploring the Limits of Quantum Nonlocality
(PhysOrg.com) -- When it comes to nonlocal correlations, some correlations are more nonlocal than others. As the subject of study for several decades, nonlocal correlations (for example, quantum entanglement) exist between two objects when they can somehow directly influence each other even when separated by a large distance. Because these correlations require “passion-at-a-distance” (a term coined by physicist Abner Shimony), they violate the principle of locality, which states that nothing can travel faster than the speed of light (even though quantum correlations cannot be used to communicate faster than the speed of light). Besides being a fascinating phenomenon, nonlocality can also lead to powerful techniques in computing, cryptography, and information processing.
Quantum Limits
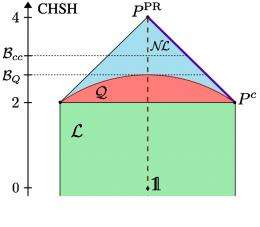
Despite advances in quantum research, physicists still don’t fully understand the fundamental nature of nonlocality. In 1980, mathematician Boris Tsirelson found that quantum correlations are bounded by an upper limit; quantum nonlocality is only so strong. Later, in 1994, physicists Sandu Popescu and Daniel Rohrlich made another surprising discovery: a particular kind of correlation might exist above the “Tsirelson bound,” as well as below the bound, in a certain range (see image). These so-called post-quantum correlations are therefore “more nonlocal” than quantum correlations.
“Tsirelson's bound represents the most nonlocal ‘boxes’ that can be created with quantum mechanics,” Nicolas Brunner, a physicist at the University of Bristol, told PhysOrg.com. “Nonlocality here is measured by the degree of violation of a Bell inequality. So, quantum non-locality appears to be limited. The big question is why. That is, is there a good physical reason why post-quantum correlations don’t seem to exist in nature?”
In a recent study, Brunner and coauthor Paul Skrzypczyk, also of the University of Bristol, propose an explanation for why post-quantum correlations are unlikely to exist, which may reveal insight into why quantum nonlocality is bounded, as well as into the underlying difference between quantum and post-quantum correlations.
In their study, Brunner and Skrzypczyk have shown that a certain class of post-quantum correlations is unlikely to exist due to the fact that it makes communication complexity trivial. This triviality occurs due to the fact that the nonlocality of these correlations can be enhanced beyond a critical limit, and - surprisingly - in spite of the fact that some of these correlations are arbitrarily close to classical correlations (they give an arbitrarily small violation of Bell’s inequality). As previous research has suggested, any theory in which communication complexity is trivial is very unlikely to exist.
Beyond Quantum
“’Post-quantum’ means beyond quantum,” Brunner explained. “This term applies to correlations, which are conveniently - and probably most simply - described by ‘black boxes.’ The basic idea is the following: imagine a black box shared by two distant parties Alice and Bob; each party is allowed to ask a question to the box (or make a measurement on the box, if you prefer) and then gets an answer (a measurement outcome). By repeating this procedure many times, and at the end comparing their respective results, Alice and Bob can identify what their box is doing. For instance, it could be that the outcomes are always the same whenever Alice and Bob choose the same questions. This kind of behavior is a correlation; knowing one outcome, it is possible to deduce the other one, since both outcomes are correlated.
“Now, it happens that there exist different types of correlations; basically those that can be understood with classical physics (where correlations originate from a common cause), and those that cannot. This second type of correlation is called nonlocal, in the sense that it cannot be explained by a common cause. A priori it is not obvious to tell whether some correlations are local or not. The way physicists can tell this is by testing a Bell inequality; when a Bell inequality is violated, then the correlations cannot be local; that is, there cannot exist a common cause to these correlations.
“Now, an amazing thing about quantum mechanics is that it allows one to construct boxes that are non-local. This is quantum nonlocality. Now, it happens that not all nonlocal boxes can be constructed in quantum mechanics. Thus there exist correlations which are unobtainable in quantum mechanics. These are called post-quantum correlations. In general, post-quantum correlations can be above Tsirelson’s bound, but in some very specific cases, they can also be below.”
‘Distilling’ Post-Quantum Nonlocality
To demonstrate that post-quantum correlations cannot exist in nature, Brunner and Skrzypczyk developed a protocol for deterministically distilling nonlocality in post-quantum states. That is, the technique refines weakly nonlocal states into states with greater nonlocality. In this context, “distillation” can also be thought of as “purifying,” “amplifying,” or “maximizing” the nonlocality of post-quantum correlations. Since nonlocal correlations are more useful if they are stronger, maximizing nonlocality has significant implications for quantum information protocols. The physicists’ protocol works specifically with “correlated nonlocal boxes,” which are a particular class of post-quantum boxes.
Brunner and Skrzypczyk’s distillation protocol builds on a recent breakthrough by another team (Forster et al.), who presented the first nonlocality distillation protocol just a few months ago. However, the Forster protocol can distill correlated nonlocal boxes only up to a certain point, violating a Bell inequality called the Clauser-Horne-Shimony-Holt (CHSH) inequality only up to CHSH = 3. While this value is greater than Tsirelson’s bound of 2.82, it does not reach the bound of 3.26, which marks the point at which communication complexity becomes trivial.
Taking a step forward, Brunner and Skrzypczyk’s protocol can distill nonlocality all the way up to the maximum nonlocality of the Popescu-Rohrlich box, which is 4. In passing the 3.26 bound of triviality, they show that these post-quantum correlated nonlocal boxes do indeed collapse communication complexity.
The distillation protocol is executed by two distant parties that share two weakly correlated nonlocal boxes. Each party can input one bit into a box to receive one output bit, simulating a binary input/binary output system with local operations. As the scientists explain, a distillation protocol can be viewed as a way of classically wiring the two boxes together. The protocol is a choice of four wirings, one for each input of Alice and Bob. The wiring (algorithm) that determines the outbit bits of the boxes will transform the two nonlocal boxes into a single correlated nonlocal box, which has stronger nonlocality than the two individual boxes.
Importantly, this protocol can distill any correlated nonlocal box that violates the CHSH inequality by less than a limit of 3.26 to more than 3.26. In other words, any correlated nonlocal box that has not previously made communication complexity trivial can be made to do so. Surprisingly, some of these boxes can even be arbitrarily close to being classical (below or equal to 2), and yet, since they can be distilled beyond the “bound of triviality,” they still collapse communication complexity. According to previous studies of triviality, such boxes are very unlikely to exist - even those below Tsirelson’s bound.
Trivial Complexity
Theoretically, when communication complexity is trivial, even the most complex problems can be solved with a minimum amount of communication. In the following example, Brunner explains what would happen in real life if a single bit of information could solve any problem.
“Communication complexity is an information processing task,” Brunner said. “Here is an example. Suppose you and I would like to meet during the next year; so given our respective agendas, we would like to know whether there is a day where both of us are free or whether there is not; doesn’t matter what that day is, we just want to know whether there is such a day or not.
Since we are in distant locations, we must send each other some information to solve the problem. For instance, if I send you the whole information about my agenda, then you could find out whether a meeting is possible or not (and so solve the problem). But indeed that implies that I should send you a significant quantity of information (many bits). It turns out that in classical physics (or, if you prefer, in everyday life), there is no better strategy; I really have to send you all that information. In quantum physics, though there exist stronger correlations than in classical physics (quantum nonlocal correlations), I would still have to send you an enormous amount of communication.
“Now, the really astonishing thing is that, if you have access to certain post-quantum correlations (post-quantum boxes), a single bit of communication is enough to solve this problem! In other words, communication complexity becomes trivial in these theories, since one bit of communication is enough to solve any problem like this one. Importantly, in classical or quantum physics, communication complexity is not trivial. More generally, for computer scientists, a world in which communication complexity becomes trivial is highly unlikely to exist. Previously, it was known that post-quantum boxes with a very high degree of violation of a Bell inequality make communication complexity trivial; now, the astonishing thing about our result is that we show that some correlations with a very small degree of violation of a Bell inequality - but indeed not accessible with quantum mechanics - can also make communication complexity trivial.”
Post-Quantum Future
In the future, Brunner and Skrzypczyk hope to find improved distillation protocols that might work for a wider variety of post-quantum nonlocal boxes, not only correlated nonlocal boxes. More research is also needed to explain why quantum correlations cannot exist in the gap between Tsirelson’s bound and the bound of triviality. Ultimately, this line of research could help make a distinction between quantum and post-quantum correlations, with important theoretic implications.
“The greatest implications of our results are the following,” Brunner said. “First, they give new evidence that certain post-quantum theories allow for a dramatic increase in communication power compared to quantum mechanics, and therefore appear very unlikely to exist in nature. The nice thing, in particular, is that some of these theories allow only for little nonlocality (as measured by the degree of violation of a Bell inequality). Thus our result is a striking demonstration that we still have no clue on how to correctly measure nonlocality. Finally, it is one step further towards an information-theoretic axiom for quantum mechanics.”
More information: Nicolas Brunner and Paul Skrzypczyk. “Nonlocality Distillation and Postquantum Theories with Trivial Communication Complexity.” Physical Review Letters 102, 160403 (2009).
Copyright 2009 PhysOrg.com.
All rights reserved. This material may not be published, broadcast, rewritten or redistributed in whole or part without the express written permission of PhysOrg.com.