Two Brains - One Thought
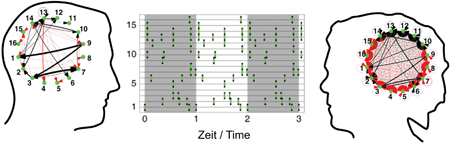
Although no two brains are alike, they can display a comparable pattern of neural activity when exposed to similar sensory input. Scientists at the Max Planck Institute for Dynamics and Self-Organization in Göttingen have now developed a mathematical method to design networks from neural cells which exhibit a predefined pattern dynamics. The researchers hope that their method will assist them in getting closer to understanding which of the possible network configurations was privileged by evolution - and why (Physica D: Nonlinear Phenomena, December, 2006).
The nerve cells of the brain are inter-connected to a complex network. All brain activities are the result of the "firing" of nerve cells, when they send electrical pulses - like a Morse code - to other cells of the brain. This process depends on the exact dynamics of the neuronal activity. When the brain receives sensory input, calculates or remembers, it processes information encoded in a series of neuronal impulses in different nerve cells.
Although no two people have the same brain, they can still share the same thought. Thus, only to a certain extent is the dynamics of neuronal activity dependent on the structure of neuronal networks. For networks far simpler than that of the human brain this idea also applies: different structures can display the same functionality.
Raoul-Martin Memmesheimer and Marc Timme, researchers at the Max Planck Institute for Dynamics and Self-Organization and the Bernstein Center for Computational Neuroscience Göttingen, have developed a mathematical method to describe the set of all networks that exhibit a given dynamics. With this, they provide researchers with a tool which can be used to investigate the correlation between structure and function of a neuronal network.
A common approach in scientific research is to investigate the structure of a system in order to then draw conclusions about its function. Memmesheimer and Timme now took the reverse perspective. "For some simple networks we know the activity dynamics, that is, their function, but not their exact structure", explains Memmesheimer. "Any given dynamics can normally be created by a variety of different networks. We have developed a method to mathematically pin down this diversity".
This procedure resembles juggling with many unknown quantities and requires great computational power. Already in a network of 1000 neurons (where each neuron can be connected to any other) there are a million possible contacts between any two neurons and consequently an unimaginably large number of possible networks. Each combination can have either an inhibiting or an activating effect on the downstream neuron and, in addition to this, can differ in its intensity and reaction time.
The entirety of all possible networks of a defined dynamics resembles a complex figure in a multidimensional space. Here, every point on the surface specifies the data required to determine a network with the desired dynamics. Memmesheimer and Timme have now worked out a mathematical description for this figure.
The researchers examined the applicability of their model on the basis of a concrete question. They calculated all possible networks that generate a given dynamics and simultaneously fulfil a further condition: the structure of the network should be as simple as possible, that is, the number of connections and the strength of the synapses should be minimal. "Applied to a real network, one could for example analyse which structural optimisation principles function in evolution", says Timme.
The dynamics of a number of very simple networks that generate repetitive patterns - like the insect walking pattern - are already well-understood. Has evolutionary pressure kept the structural complexity of such networks to a minimum - or could there have been other networks with an even simpler structure, yet possessing the same dynamics? Is it possible that many more networks fulfilling the same functional and structural conditions could have evolved?
There is still no definite answer to these puzzles; however, with the help of the new methods developed by Memmesheimer and Timme, we are a step closer towards understanding them.
Citation:
-- R.-M.Memmesheimer, M. Timme, Designing complex networks, Physica D: Nonlinear Phenomena, December, 2006
-- R.-M.Memmesheimer, M. Timme, Designing the Dynamics of Spiking Neural Networks, Physical Review Letters, November 3rd, 2006
Source: Max-Planck-Institute for Dynamics and Self-Organization