Scent explained mathematically

(PhysOrg.com) -- An interdisciplinary team of neurobiologists and mathematicians from the Friedrich Miescher Institute for Biomedical Research (FMI, Switzerland) has managed to mathematically describe an important basic computation in the brain: pattern decorrelation. Their mathematical model provides a sound explanation for former observations in the olfactory bulb. The results have been published recently in the renowned scientific journal Nature Neuroscience.
When Carl Friedrich Gauss calculated the orbit and predicted the exact position of the dwarf planet Ceres in 1801 based on data collected by astronomer Giuseppe Piazzi, Europe was in awe. Gauss' ability to mathematically describe a natural phenomenon inspired people much more than his equally brilliant number theory. Two hundred years later, orbital prediction and astronomical computation are no longer such a tough nut to crack. But many biological processes, such as cognitive processes in the brain, are still elusive to mathematical description and hence a deeper understanding.
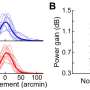
Now, the small team of neurobiologists and mathematicians managed to mathematically understand pattern decorrelation, a fundamental computation in the brain, which also has many applications in computer science and engineering. Previously, the group at FMI studied decorrelation in the olfactory system and found that it makes representations of odors in the brain more distinct. Without decorrelation, discriminating odors would be much more cumbersome. However, the mechanisms underlying decorrelation are complicated by non-linearity and so-called recurrent connectivity through which neurons can influence each other in a complex fashion. So far, the meaning of this arrangement has not been understood.
Martin Wiechert, the mathematician in Rainer Friedrich's group, has now cracked this problem. His mathematical theory, published in Nature Neuroscience, shows that decorrelation emerges naturally from two features of recurrent neuronal circuits: sparse connections and high spontaneous activity.
"We have known for a while from observations that activity is high and connectivity sparse within the olfactory bulb. But we did not know why this is the case," comments Rainer Friedrich, FMI Group Leader and supervisor of the study. "Our mathematical results allow us to explain not only the structure of neuronal circuits in the olfactory bulb but also to understand better what happens when we smell."
Biologically relevant processes are difficult to explain mathematically not merely because of their complexity, but also because the data necessary to test the mathematical principles is often missing. "Our laboratory is uniquely predisposed for such a study. We have been able to measure activity in individual neurons very efficiently with optical methods for a while now. Such data is crucial to develop mathematical circuit models," explains Friedrich. "As the project progressed, experimentation and mathematical model development cross-fertilized each other. Based on the mathematical studies we devised experiments and were able to provide the data to confirm or rebut mathematical reasoning. In exchange, we received mathematically validated information on how neuronal circuits work."
While mechanisms of decorrelation are now understood, other neuronal processes such as learning or memory still await mathematical explanation. Rainer Friedrich's lab is perfectly equipped to address these questions as well.
More information: Publication in Nature Neuroscience www.nature.com/neuro/journal/v … rent/pdf/nn.2591.pdf