Quantum Walk in Laboratory

A team of physicists headed by Christian Roos and Rainer Blatt from the Institute of Quantum Optics and Quantum Information of the Austrian Academy of Sciences realize a quantum walk in a quantum system with up to 23 steps. It is the first time that this quantum process using trapped ions is demonstrated in detail.
When a hiker comes to a junction s/he has to decide which way to take. All of these decisions, eventually, lead the hiker to the intended destination. When the hiker forgot the map, s/he has to make a decision randomly and gets to the destination with more or less detours. In science this is called a random walk and can regularly be encountered in mathematics and physics.
In 1827, for example, the Scottish botanist Robert Brown found out that pollen grains show irregular fluttering vibrations on water drops. This effect is caused by a random motion of water molecules - a phenomenon known in the scientific world as Brownian motion. Another example is the Galton board, which is used to demonstrate binomial distribution to students. On this board, balls are dropped from the top and they repeatedly bounce either left or right in a random way as they hit pins stuck in the board.
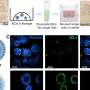
The Innsbruck scientists have now transferred this principle of random walk to quantum systems and stimulated an atom to take a quantum walk: "We trap a single atom in an electromagnetic ion trap and cool it to prepare it in the ground state," explains Christian Roos from the Institute of Quantum Optics and Quantum Information (IQOQI). "We then create a quantum mechanical superposition of two inner states and send the atom on a walk." The two internal states correspond to the decision of the hiker to go left or right. However, unlike the hiker the atom does not really have to decide where to go; due to the superposition of the two states, both possibilities are presented at the same time.
"Depending on the internal state, we shift the ion to the right or to the left," explains Christian Roos. "Thereby, the motional and internal state of the ion are entangled." After each step the experimental physicists modify the superposition of the inner states by a laser pulse and again shift the ion to the left or right. The physicists can repeat this randomly controlled process up to 23 times, while collecting data about how quantum walks work. By using a second ion, the scientists extend the experiment, giving the walking ion the additional possibility to stay instead of moving to the right or left.
The statistic analysis of these numerous steps confirms that quantum walks differ from classical (random) walks. While, for example, the balls of a Galton board move away from the starting point statistically very slowly, quantum particles spread much faster on their walk.
These experiments, which have also been realized in a similar way in Bonn, Munich and Erlangen with atoms, ions and photons, can be applied to studying natural phenomena. For example, researchers suspect that the energy transport in plants works more efficiently because of quantum walks than would be the case with classical walks. In addition, a regime of quantum walk is of importance for developing a quantum computer model, which could solve ubiquitous problems. For example, applying quantum walks in such a model would help in finding search quantum algorithms that outperform their classical counterparts as different directions could be chosen simultaneously.
More information: Realization of a quantum walk with one and two trapped ions. Zähringer F, Kirchmair G, Gerritsma R, Solano E, Blatt R, Roos CF. Phys. Rev. Lett. 104, 100503 (2010). dx.doi.org/10.1103/PhysRevLett.104.100503
Provided by Austrian Academy of Sciences