New tool enables powerful data analysis
(PhysOrg.com) -- A powerful computing tool that allows scientists to extract features and patterns from enormously large and complex sets of raw data has been developed by scientists at University of California, Davis, and Lawrence Livermore National Laboratory. The tool - a set of problem-solving calculations known as an algorithm - is compact enough to run on computers with as little as two gigabytes of memory.
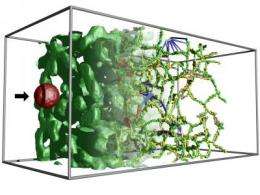
The team that developed this algorithm has already used it to probe a slew of phenomena represented by billions of data points, including analyzing and creating images of flame surfaces; searching for clusters and voids in a virtual universe experiment; and identifying and tracking pockets of fluid in a simulated mixing of two fluids.
"What we've developed is a workable system of handling any data in any dimension," said Attila Gyulassy, who led the five-year development effort while pursuing a PhD in computer science at UC Davis. "We expect this algorithm will become an integral part of a scientist's toolbox to answer questions about data."
A paper describing the new algorithm was published in the November-December issue of IEEE Transactions on Visualization and Computer Graphics.
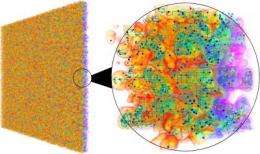
Computers are widely used to perform simulations of real-world phenomena and to capture results of physical experiments and observations, storing this information as collections of numbers. But as the size of these data sets has burgeoned, hand-in-hand with computer capacity, analysis has grown increasingly difficult.
A mathematical tool to extract and visualize useful features from data sets has existed for nearly 40 years - in theory. Called the Morse-Smale complex, it partitions sets by similarity of features and encodes them into mathematical terms. But working with the Morse-Smale complex is not easy. "It's a powerful language. But a cost of that, is that using it meaningfully for practical applications is very difficult," Gyulassy said.
Gyulassy's algorithm divides data sets into parcels of cells, then analyzes each parcel separately using the Morse-Smale complex. Results of those computations are then merged together. As new parcels are created from merged parcels, they are analyzed and merged yet again. At each step, data that do not need to be stored in memory are discarded, drastically reducing the computing power required to run the calculations.
One of Gyulassy's tests of the algorithm was to use it to analyze and track the formation and movement of pockets of fluid in the simulated mixing of two fluids: one dense, one light. The complexity of this data set is so vast - it consists of more than one billion data points on a three-dimensional grid - it challenges even supercomputers, Gyulassy said. Yet the new algorithm with its streamlining features was able to perform the analysis on a laptop computer with just two gigabytes of memory. Although Gyulassy had to wait nearly 24 hours for the little machine to complete its calculations, at the end of this process he could pull up images in mere seconds to illustrate phenomena he was interested in, such as the branching of fluid pockets in the mixture.
Two main factors are driving the need for analysis of large data sets, said co-author Bernd Hamann: a surge in the use of powerful computers that can produce huge amounts of data, and an upswing in affordability and availability of sensing devices that researchers deploy in the field and lab to collect a profusion of data.
"Our data files are becoming larger and larger, while the scientist has less and less time to understand them," said Hamann, a professor of computer science and associate vice chancellor for research at UC Davis. "But what are the data good for if we don't have the means of applying mathematically sound and computationally efficient computer analysis tools to look for what is captured in them?"
Gyulassy is currently developing software that will allow others to put the algorithm to use. He expects the learning curve to be steep for this open-source product, "but if you just learn the minimal amount about what a Morse-Smale complex is," he said, "it will be pretty intuitive."
Source: University of California - Davis