Math Models Snowflakes

Three-dimensional snowflakes can now be grown in a computer using a program developed by mathematicians at UC Davis and the University of Wisconsin-Madison.
No two snowflakes are truly alike, but they can be very similar to each other, said Janko Gravner, a mathematics professor at UC Davis. Why they are not more different from each other is a mystery, Gravner said. Being able to model the process might answer some of these questions.
Intricate, incredibly variable and beautiful, snowflakes have been puzzling mathematicians since at least 1611, when Johannes Kepler predicted that the six-pointed structure would reflect an underlying crystal structure.
Snowflakes grow from water vapor around some kind of nucleus, such as a bit of dust. The surface of the growing crystal is a complex, semi-liquid layer where water molecules from the surrounding vapor can attach or detach. Water molecules are more likely to attach at concavities in the crystal shape.
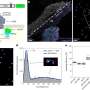
The model built by Gravner and David Griffeath of the University of Wisconsin-Madison takes these factors, as well as temperature, atmospheric pressure and water vapor density, into account. By running the model under different conditions, the researchers were able to recreate a wide range of natural snowflake shapes.
Rather than trying to model every water molecule, it divides the space into three-dimensional chunks one micrometer across. The program takes about 24 hours to produce one "snowfake" on a modern desktop computer.
As in the real world, needles are the most common pattern of computer-generated snowflake. The classic six-pointed "dendritic" or feathery snowflake is relatively rare, both in the computer simulation and in nature.
Gravner and Griffeath also managed to generate some novel snowflakes, such as a "butterflake" that looks like three butterflies stuck together along the body. Gravner said there seemed to be no reason these shapes could not appear in nature, but they would be very fragile and unstable.
One surprise was that three-dimensional structure is often important, with complex structures often growing between two plates -- a feature that is difficult to see when observing actual snowflakes, but has been observed in careful studies of real snowflakes with electron microscopes.
A paper describing the model has been submitted for publication.
Images and movies of snowflake growth models: psoup.math.wisc.edu/Snowfakes.htm
Source: University of California - Davis