January 8, 2016 feature
Musical melodies obey same laws as foraging animals
(Phys.org)—Most people think of music as more of an art than a science. Although sound is a wave, and can therefore be described by the laws of physics, understanding how certain patterns of sound waves create what we perceive as music requires a much higher-level perspective than merely understanding the properties of waves.
Despite the complexity of music, recent research has shown that music can be analyzed using some of the same physics models commonly used to describe more traditional physics concepts.
More evidence of this ability to describe music with physics comes from a new paper published in EPL by Gunnar A. Niklasson, an engineering professor at Uppsala University, Sweden, and Maria H. Niklasson, a musician at the Betel Music Institute in Bromma, Sweden.
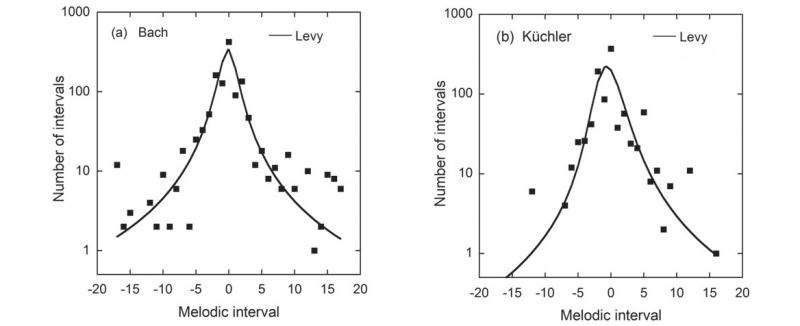
The researchers found that the distribution of melodic intervals in two classical concertos and two folk songs can be modeled by a Lévy distribution. They explain that melodic intervals are the pitch intervals between successive time intervals, which are defined by the duration of the shortest note—so each note may be equal to one or more of these time intervals. (A pitch interval can also be roughly thought of as how far apart two notes are on a piano.) The Lévy distribution describes many other diverse scenarios, such as the turbulent motion of a particle in a liquid or gas, the changes in the price of a stock, earthquake activity, and the foraging paths of wild animals.
"Our work indicates a consonance between patterns in music and in nature, but how to interpret this is more of a philosophical question," Gunnar Niklasson told Phys.org.
All Lévy motions are characterized by a mix of many short and a few long steps, and also exhibit fractal properties. For a musical melody, this basically means that there are many small intervals (just one or two notes apart) and fewer large intervals (sometimes up to 20 notes apart), and that the numbers of these intervals are distributed in the shape of a sharp peak with long tails on both sides. Previous research has implicitly assumed that melodic intervals follow a Gaussian distribution (i.e., a "bell curve"), but a Levy distribution is different from a Gaussian one, so the new results challenge these assumptions.
The researchers emphasize that the Lévy distribution is only an approximate description of the distribution of melodic intervals, as the actual distribution of intervals deviates from a perfect Lévy distribution in certain ways. One example is that, in many songs, two-note intervals are more common than one-note intervals. There are also large fluctuations in the tail regions, where the intervals are largest. The researchers suggest that some of these deviations may reflect different music styles, genres, and composers.
Besides contributing to a greater fundamental understanding of music, the findings here may also be useful for experimenting with computer-generated music.
"Computer-generated music is a very small portion of all present music," Gunnar Niklasson said. "It is my understanding that algorithms are mainly used by some composers for generating ideas that they can incorporate into new written compositions. We have not explored the relation of our work to algorithmic composition yet. However, it is interesting to note that some of the currently used algorithms are based on fractals and chaos theory."
In the future, the researchers hope to develop more automated methods of analysis, which is necessary in order to analyze larger numbers of music samples. This would also allow for a comparison of the styles of different composers, as well as a comparison of written music with computer-generated compositions.
More information: Gunnar A. Niklasson and Maria H. Niklasson. "Non-Gaussian distributions of melodic intervals in music: The Lévy-stable approximation." EPL. DOI: 10.1209/0295-5075/112/40003
Journal information: Europhysics Letters (EPL)
© 2016 Phys.org