Isolating and controlling qubits for quantum information processing
Harnessing quantum systems for information processing will require controlling large numbers of basic building blocks called qubits. The qubits must be isolated, and in most cases cooled such that, among other things, errors in qubit operations do not overwhelm the system, rendering it useless. Led by JQI Fellow Christopher Monroe, physicists have recently demonstrated important steps towards implementing a proposed type of gate, which does not rely on super-cooling their ion qubits. This work, published as an Editor's Suggestion in Physical Review Letters, implements ultrafast sensing and control of an ion's motion, which is required to realize these hot gates. Notably, this experiment demonstrates thermometry over an unprecedented range of temperatures—from zero-point to room temperature.
Graduate student and first author Kale Johnson explains how this research could be applied, "Atomic clock states found in ions make the most pristine quantum bits, but the speed at which we have been able to access them in a useful way for quantum information processing is slower than it could be. We are changing that by making each operation on the qubit faster while eliminating the need to cool the ion to the ground state after each operation."
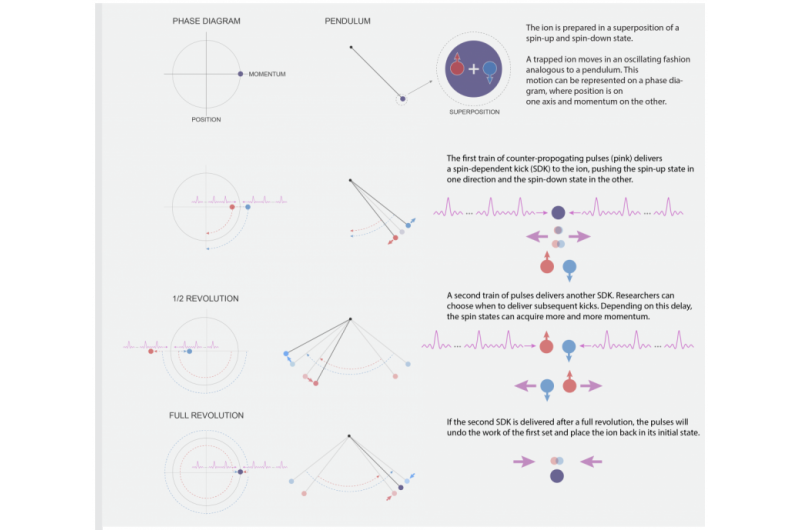
In the experiment the team begins with a single trapped atomic ion. The ion can be thought of as a bar magnet that can be oriented with its north pole 'up' or 'down' or any combination between the two poles (pointing horizontally along an imaginary equator is up + down). Physicists can use lasers and microwave radiation to control this orientation. The individual laser pulses are a mere ten picoseconds in length—a time scale that is a tiny fraction of how long it takes for the ion to undergo appreciable motion in the trap. Operating in this regime is precisely what allows researchers to have superior sensing and ultimately control over the ion motion. The speed enables the team to extract the motional behavior of an ion using a technique that works independently of the energy in the motion itself. In other words, the measurement is equally sensitive to a fast or very slow atom.
The researchers use a method that is based on Ramsey interferometry, named for the Nobel Laureate Norman Ramsey who pioneered it back in 1949. Known then as his "method of separated oscillatory fields," it is used throughout atomic physics and quantum information science.
Laser pulses are carefully divided and then reunited to achieve control over the ion's spin and motion. The researchers call these laser-ion interactions 'spin-dependent kicks' (SDK) because each series of specially tailored laser pulses flips the spin, while simultaneously giving the ion a push (this is depicted in the illustration below). With each fast kick, the atom's quantum wave packet is split into two parts in under three nanoseconds. Those halves are then re-combined at different points in space and time, and the signal from the unique overlap pattern reveals how the population is distributed between the two spin states. In this experimental sequence, that distribution depends on parameters such as the number of SDKs, the time between kicks, and the initial position and speed of the ion. The team repeats this experiment to extract the average motion of the ion, or its effective temperature.
In order to realize proposed two-ion quantum gates that do not require cooling the system into its quantum mechanical ground state, multiple spin dependent kicks must be employed with high accuracy such that errors remain manageable. Here the team was able to clearly demonstrate the necessary high-quality spin dependent kicks. More broadly, this protocol shows that adding ultrafast pulsed laser technology to the ion-trapping toolbox gives physicists ultimate quantum control over what can be a limiting, noise-inducing parameter: the motion.
More information: K. G. Johnson et al. Sensing Atomic Motion from the Zero Point to Room Temperature with Ultrafast Atom Interferometry, Physical Review Letters (2015). DOI: 10.1103/PhysRevLett.115.213001
Journal information: Physical Review Letters
Provided by Joint Quantum Institute