Down in one: Simple maths shows neknomination can't last

The media are aflutter about a new drinking game. The aim of "neknomination" is to down a pint, then tell some of your friends to do the same. Or as students call it, Wednesday night.

This time, however, the results are posted online, which has raised plenty of questions. What does it tell us about drinking culture? How do social media influence things? How long will it last?

It is easy to over-analyse the social and political impact of trends, but the last question is actually an interesting one from a scientific point of view. Neknomination has all the marks of an epidemic, so it makes sense to look at the phenomenon as if it were an infection.

When faced with a new disease outbreak, there are two numbers that epidemiologists use to judge transmission. One is the reproduction number, denoted R. This is the average number of secondary cases generated by a typical infectious person.

If R is less than one, each person will produce less than one secondary case, and the infection will fizzle out into extinction. If R is greater than one, the disease could go on to cause a major outbreak. Judging by the neknominations currently littering my Facebook feed, each downed pint produces two or three nominations. Hence the reproduction number for neknomination is between two and three, similar to what it was for the 1918 influenza pandemic and 2003 SARS outbreak.

The reproduction number isn't the full story, though. When studying an outbreak, we also need to know how quickly the infection spreads. The "generation time" of an infection is the average time between an initial case displaying symptoms (or necking a pint) and the person they infect becoming symptomatic. The smaller the generation time, the faster the disease spreads. Again, neknomination is nice and easy to quantify: nominees have 24 hours to down their drink.

So what might the outbreak look like? Let us say the reproduction number is two. If we start with one downed pint, we might expect to see two the following day. These two would generate two more, making four in total. Then eight then next day, and so on. This would suggest that the amount of pint necking would increase exponentially. Within 32 days, all 7 billion people on Earth would have necked a pint and stuck the video on Facebook.

But in reality that obviously won't happen. Once someone has downed a pint, they might not be so keen to do another. In other words, the number of susceptible individuals – the people willing to play the game – declines over time.

For simplicity, let's assume that once someone has necked a pint, they won't do another. We can therefore simulate the epidemic using a so-called SIR model (this stands for Susceptible-Infective-Recovered). If we assume that 1% of a susceptible population – such as a friendship group – are infected initially, we obtain the following epidemic curve:

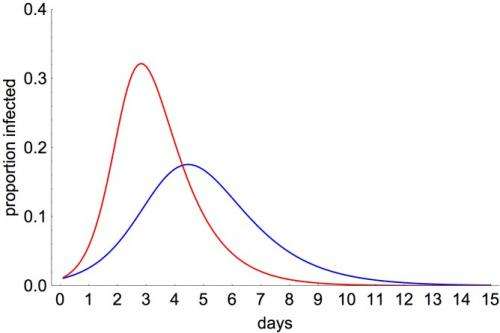
The blue line is when R=2, and the red line when R=3. In both cases, the infection burns itself out within a week or so. Note that this isn't because everyone has been infected: it is because there aren't enough susceptible people left to sustain transmission.

If we assume that people get bored of the game after necking two pints rather than one, we get a similar picture, albeit with a slightly larger outbreak:

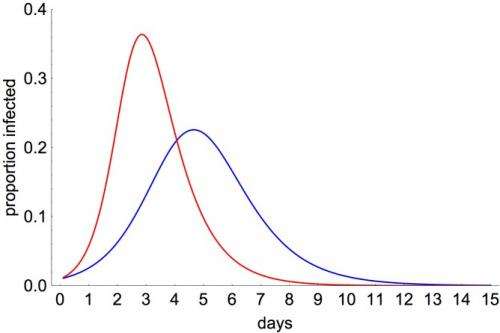
These simulations are a good starting point, but there is another factor we must consider. In the SIR model, we assume that nominations are aimed randomly at the available pool of susceptible people. In real life, however, people cluster together, and so will probably have mutual friends. This means that two people might nominate the same person. Such social network structure will reduce the reproduction number, leading to smaller outbreaks.

All this theory suggests that rather than being one large epidemic, neknomination is instead a series of smaller, independently introduced outbreaks, each of which burns out very quickly. So if you are tired of all these nominations appearing on your newsfeed, don't worry. It should all be over soon.

Disclaimer: It is worth pointing out that these are just back-of-the-envelope calculations using simple models. Hence this analysis shouldn't be taken as an exact prediction. Rather, it should be seen as a light-hearted illustration of some important concepts in disease outbreak analysis.

This story is published courtesy of The Conversation (under Creative Commons-Attribution/No derivatives).