A mathematical perspective of seasonal variations in Lyme disease transmission
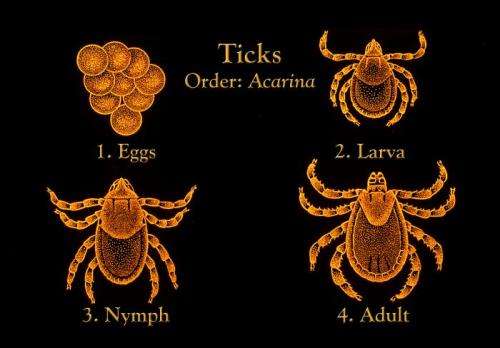
Lyme disease is a common tick-borne illness caused by a bacterium, which is transmitted to humans through the bite of infected ticks. The transmission dynamics of Lyme disease is dependent on a variety of factors, including the length of the tick's life cycle, availability of hosts, climatic conditions and seasonal influences, which are important to understand for control strategies.
In a paper published last month in the SIAM Journal on Applied Mathematics, authors Yuxiang Zhang and Xiao-Qiang Zhao propose a reaction-diffusion model to study transmission dynamics of Lyme disease while taking into account seasonality.
Ticks live for roughly 2 years, and their life cycle includes three stages: larva, nymph and adult. Ticks climb on to host animals who brush against vegetation from the tips of grasses and shrubs. Once they attach themselves, they feed on blood by inserting their mouthparts into the skin of a host, thus transmitting the disease. After obtaining a blood meal—which can take anywhere between 3 and 5 days—ticks drop off their hosts and prepare for the next stage of the life cycle.
Adult ticks feed and mate on larger mammals such as deer. After obtaining their meal, adult females drop off their hosts and lay eggs on the ground. The eggs hatch into larvae, and larval ticks feed on smaller animals such as mice and birds. After obtaining a blood meal from these smaller hosts, larvae drop off and are inactive until they grow into nymphs. Nymphs feed on small rodents, birds and other small mammals, and then molt into adults. The cycle thus repeats itself.
For Lyme disease to exist in an area, the bacteria that cause it, the ticks that carry the bacteria, and mammals that provide food to ticks in their various life stages must be present. Seasonal variations in temperature, rainfall and resource availability also affect disease transmission and dynamics.
"Ticks develop slowly or become less active in colder temperatures, and rainfall is also critically important for their development, survival, and activities," explains author Xiao-Qiang Zhao. "According to a report from the Public Health Agency of Canada on Lyme disease cases in Ontario between 1999 and 2004, most occurred in late spring and summer, when the young ticks are most active and people are outdoors more often."
A previous model proposed a reaction and diffusion model to study global dynamics of Lyme disease. A reaction-diffusion model takes into account the interaction (reaction) of constituents within the system (in this case pathogens, susceptible hosts and infective hosts) and their change in density over time within their respective populations (diffusion).
The previously-proposed spatial model treats population densities in a continuous two-dimensional space, factoring in birth, death, infection and developmental advancement. However, the model does not account for seasonal patterns.
In this paper, the authors modify this previous model into a reaction and diffusion model in a periodic environment, which models seasonable variables (eg. temperature) as a periodic function. A periodic function is one that repeats its values at regular intervals.
Since seasonal variations are critical for tick development and their activities, which are strongly affected by temperatures, the authors assume that the development rates of ticks as well as their activity rates are time-dependent. The model is governed by a periodic reaction-diffusion system that factors in the densities of susceptible and pathogen-infected mice, densities of susceptible and infectious larvae and nymphs, and densities of uninfected and pathogen-infected adult ticks.
The authors introduce the basic reproduction number R0, which is the number of infectious cases one case of disease can generate on average over the course of the infectious period in a susceptible population. The authors show that R0 can serve as the threshold parameter for stability of either the disease-free or endemic steady state.
"We introduced the basic reproduction ratio R0 and obtained the global dynamics of the disease in terms of R0," says Zhao. The disease is expected to die out when R0 <1 and stabilize in a positive periodic state when R0 >1. Hence, the objective is to drive R0 to less than 1. "In the case where R0 > 1, we may get an approximate value of the infection level, and then alter some parameters to drive R0 < 1 so that the disease can be eradicated ultimately," explains Zhao.
"We also established the existence and a computational formula of the spreading speed of infection when R0 > 1," says Zhao. "To control the disease, we may use strategies to reduce the spreading speed. For example, we may use some chemical methods to reduce the infection susceptibilities or the total number of hosts."
Future research involves taking into account the time between various stages of the tick life cycle. "One future direction is to incorporate time delays between tick life stages into our model," says Zhao. "Another challenging problem is to study the spreading speeds and traveling waves in the case where some parameters are spatially dependent."
More information: A Reaction-Diffusion Lyme Disease Model with Seasonality, Yuxiang Zhang and Xiao-Qiang Zhao, SIAM Journal on Applied Mathematics, 73(6), 2077. (Online publish date: November 12, 2013). The source article is available for free access at this link until March 19, 2014: epubs.siam.org/doi/abs/10.1137/120875454
Journal information: SIAM Journal on Applied Mathematics
Provided by Society for Industrial and Applied Mathematics