Leaner Fourier transforms: Algorithm separates signals into their individual frequencies using minimal number of samples
The fast Fourier transform, one of the most important algorithms of the 20th century, revolutionized signal processing. The algorithm allowed computers to quickly perform Fourier transforms—fundamental operations that separate signals into their individual frequencies—leading to developments in audio and video engineering and digital data compression.
But ever since its development in the 1960s, computer scientists have been searching for an algorithm to better it.
Last year MIT researchers Piotr Indyk and Dina Katabi did just that, unveiling an algorithm that in some circumstances can perform Fourier transforms hundreds of times more quickly than the fast Fourier transform (FFT).
Now Indyk, a professor of computer science and engineering and a member of the Theory of Computation Group within the Computer Science and Artificial Intelligence Laboratory (CSAIL), and his team have gone a step further, significantly reducing the number of samples that must be taken from a given signal in order to perform a Fourier transform operation.
Close to theoretical minimum
In a paper to be presented at the ACM-SIAM Symposium on Discrete Algorithms in January, Indyk, postdoc Michael Kapralov, and former student Eric Price will reveal an algorithm that can perform Fourier transforms using close to the theoretical minimum number of samples. They have also bettered even this, developing an algorithm that uses the minimum possible number of signal samples.
This could significantly reduce the time it takes medical devices such as magnetic resonance imaging (MRI) and nuclear magnetic resonance (NMR) machines to scan patients, or allow astronomers to take more detailed images of the universe, Indyk says.
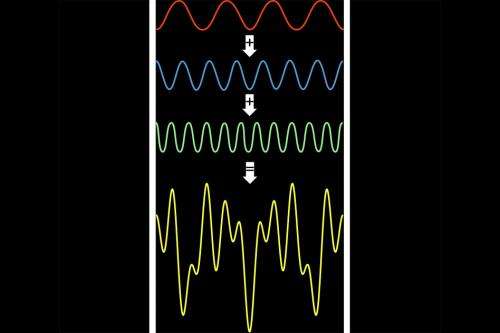
The Fourier transform is a fundamental mathematical notion that allows signals to be broken down into their component parts. When you listen to someone speak, for example, you can hear a dominant tone, which is the principal frequency in their voice. "But there are many other underlying frequencies, which is why the human voice is not a single tone, it's much richer than that," Indyk says. "So in order to understand what the spectrum looks like, we need to decompose the sounds into their basic frequencies, and that is exactly what the Fourier transform does."
The development of the FFT automated this process for the first time, allowing computers to rapidly manipulate and compress digital signals into a more manageable form. This is possible because not all of the frequencies within a digital signal are equal. Indeed, in nature many signals contain just a few dominant frequencies and a number of far less important ones, which can be safely disregarded. These are known as sparse signals.
"In real life, often when you look at a signal, there are only a small number of frequencies that dominate the spectrum," Indyk says. "So we can compress [the signal] by keeping only the top 10 percent of these."
Indyk and Katabi's previous work focused on the length of time their algorithm needed to perform a sparse Fourier transform operation. However, in many applications, the number of samples the algorithm must take of the signal can be as important as its running time.
Applications in medical imaging, astronomy
One such example is in MRI scanning, Indyk says. "The device acquires Fourier samples, basically snapshots of the body lying inside the machine, which it uses to recover the inner structure of the body," he says. "In this situation, the number of samples taken is directly proportionate to the amount of time that the patient has to spend in the machine."
So by allowing the MRI scanner to produce an image of the body using a fraction of the samples needed by existing devices, it could significantly reduce the time patients must spend lying still inside the narrow, noisy machines.
The team is also investigating the idea of using the new sparse Fourier transform algorithm in astronomy. They are working with researchers at the MIT Haystack Observatory, who specialize in radio astronomy, to use the system in interferometry, in which signals from an array of telescopes are combined to produce a single, high-resolution image of space. Applying the sparse Fourier transform algorithm to the telescope signals would reduce the number of observations needed to produce an image of the same quality, Indyk says.
"That's important," he says, "because these are really massive data sets, and to make matters worse, much of this data is distributed because there are several different, separated telescopes, and each of them acquires some of the information, and then it all has to be sent to the same place to be processed."
What's more, radio telescopes are extremely expensive to build, so an algorithm that allows astronomers to use fewer of them, or to obtain better quality images from the same number of sensors, could be extremely important, he says.
Martin Strauss, a professor of mathematics, electrical engineering, and computer science at the University of Michigan, who develops fundamental algorithms for applications such as signal processing and massive data sets, says work by Indyk and others makes sparse Fourier transform algorithms advantageous over the celebrated FFT on a larger class of problems than before. "The current paper squeezes out nearly all [of the performance] that is possible with these methods," he says.
Provided by Massachusetts Institute of Technology
This story is republished courtesy of MIT News (web.mit.edu/newsoffice/), a popular site that covers news about MIT research, innovation and teaching.