Elucidating biological cells' transport mechanisms
A new study focuses on the motion of motor proteins in living cells, applying a physicist's tool called non-equilibrium statistical mechanics
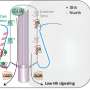
Motion fascinates physicists. It becomes even more intriguing when observed in vivo in biological cells. Using an ingenious setup, Japanese scientists have now calculated the force of molecular motors acting on inner components of biological cells, known as organelles. In a new study, published in EPJ E, the focus is on mitochondria - akin to micrometric range cellular power plants - travelling along microtubules in a cell. These findings by Kumiko Hayashi, from Tohoku University, Sendai, Japan, and team could contribute to elucidating the transport mechanism in biological cells by multiple motors.
Hayashi and colleagues have investigated, for the first time, the so-called Einstein relation for the motion of mitochondria transported by motor proteins - called kinesin and dynein - in living cells. The Einstein relation describes how micro-sized beads follow a random motion under the influence of thermal noise, when diffusing in aqueous solutions. This relation stems from the fluctuation dissipation theorem studied in the field of non-equilibrium statistical mechanics.
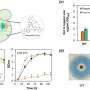
The researchers observed the motion of a mitochondrion transported by motor proteins using fluorescence microscopy. They applied a single-particle tracking algorithm to the images of fluorescently tagged mitochondria. They then compared this motion with the random motion of a bead artificially incorporated into a cell, observed by using fluorescence correlation spectroscopy.
By comparing both evaluations of the diffusion coefficient, from both mitochondria and bead estimates, they found that the value of the medium's viscosity obtained using the beads was slightly lower than that obtained using the organelle motion. This discrepancy is linked to the fact that physical laws such as the Einstein relation are not sufficient to fully describe the organelles' motion, which is subjected to many simultaneous complex biological processes, such as the chemical reaction of motor proteins and the interaction with the cell's vesicles.
More information: K. Hayashi et al. (2013), Viscosity and drag force involved in organelle transport: Investigation of the fluctuation dissipation theorem, European Physical Journal E 36: 136, DOI: 10.1140/epje/i2013-13136-6
Journal information: European Physical Journal E , European Physical Journal
Provided by Springer