The 12 days of Pascal's triangular Christmas

One of the most magical aspects of mathematics is the ability for complex and intricate structures to emerge from the simplest of rules. Few mathematical objects are simpler to create – and few weave such a variety of intricate patterns – as Pascal's marvellous triangle.
To make your own Pascal's triangle, all you need is a pen and paper and one very simple rule – each number in the triangle is the sum of the two numbers directly above it. Line the numbers up like bricks in a wall, put 1s down the outside of each row, and add – like so:

Blaise Pascal was a 17th century French mathematician. He was primarily interested in using the triangle to advance his studies in probability theory – a field which he more or less invented in correspondence with Pierre de Fermat, after a gambling friend asked Pascal for advice on how two dice players should divide up the pot if their game was interrupted early.
Although simple to make, the triangle hides many, many surprising patterns. So, with apologies to folk carols in general and Frederic Austin in particular…
On the first day of Christmas, the triangle gave to me…
Counting numbers (with symmetry)
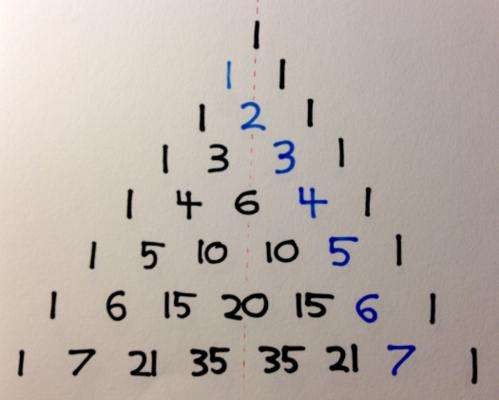
The two most immediate patterns that tumble out of the triangle are its bilateral symmetry – the left and right halves of the tree mirror each other perfectly – and the sight of the familiar counting numbers marching down the inner diagonals on each side.
On the second day of Christmas, the triangle gave to me…
Powers of two

Adding all the numbers across each row will reveal all the powers of two (and shows that 2 to the power of 0 really wants to be equal to 1).
On the third day of Christmas, the triangle gave to me…
Triangular numbers
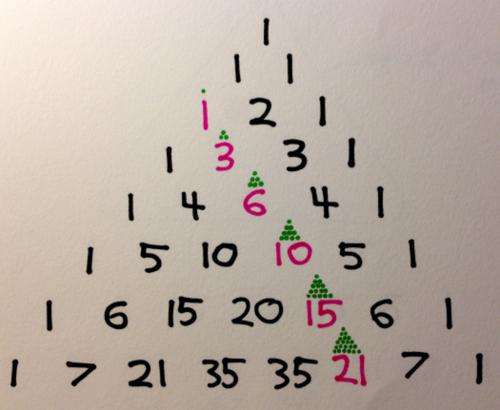
We've already seen the counting numbers along the first inner diagonal – now let's turn our attention to the second diagonal. Suppose you're baking Christmas goodies for friends and family this year and you have triangles on your mind. How many treats will you need to bake so that you can later arrange them in a triangular pattern?
Technically one treat will do, but that's what mathematicians would call a trivial triangle (your friends might use a more colourful term). Three would be nicer.
You could grow your gift triangle by adding another three (for a total of six) beneath your original small triangle – or still further by adding another four (for a total of ten).
The numbers that hit the sweet spot for creating triangles are appropriately named triangular numbers, and they appear down the second inner diagonals on each side.
On the fourth day of Christmas, the triangle gave to me…
Fibonacci

The sequence of Fibonacci's numbers starts with 1 and 1, then each subsequent number is the sum of the two numbers that came immediately before it. They were first described in 1202 by Fibonacci (or Leonardo of Pisa), in the context of rabbits who could perform multiplication rapidly.
They're tricky to spot in Pascal's triangle, but they can be coaxed out of hiding! You can find them scattered across the "short diagonals" of the triangle – adding up the numbers in these short diagonals will allow you to piece Fibonacci's numbers together.
On the fifth day of Christmas, the triangle gave to me…
Prime … num-ber things!
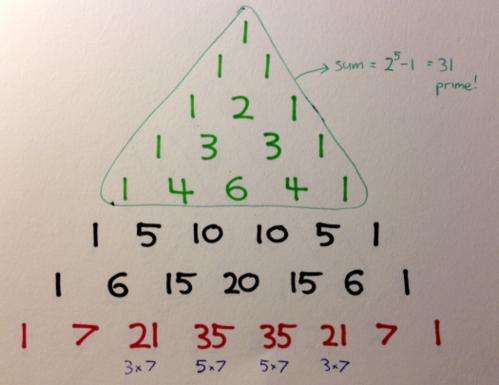
If you add up every single number in the first n rows, you'll get the nth Mersenne number (which is the number that falls 1 short of being 2 to the power of n). Mersenne numbers are used at the cutting edge of mathematical research to find really large prime numbers, because they have a very interesting feature: if n is a prime number, then every now and then the nth Mersenne number will be prime as well.
For example, adding up all the numbers in the first 5 rows of Pascal's triangle gives us the 5th Mersenne number, 31 (which is 1 less than 2 to the power of 5). Since 5 is a prime number, there's a possibility that 31 might be a prime number too… and it just so happens that it is. To date, the largest known Mersenne prime is (2 to the power of 20996011) minus 1 – a number with 6320430 digits!
Another of Pascal's prime patterns is the following – if you look at a row for which the counting number on the first inner diagonal is prime (such as 7), then every other number in that row of the triangle will be a multiple of that prime number. Except for the 1s on the outside, that is.
On the sixth day of Christmas, the triangle gave to me…
Intertwining petals

Pick any number inside Pascal's triangle and look at the six numbers around it (that form alternating petals in the flowers drawn above). If you multiply the numbers in every second petal, you'll end up with the same answer no matter which of the petals you start from.
On the seventh day of Christmas, the triangle gave to me…
Hockey-stick addition

Starting from any of the 1s on the outermost edge, add together as many numbers as you like down one of the diagonals. Wherever you stop, you'll find your sum is waiting just one diagonal step further – in the opposite direction to where you were heading (hence the "hockey-stick" pattern).
On the eighth day of Christmas, the triangle gave to me…
Squaring through addition

Pick any counting number from along the first diagonal and square it. Then look at its two neighbours that lie deeper inside the triangle – they'll always add up to that very same square number.
On the ninth day of Christmas, the triangle gave to me…
Binomial coefficients
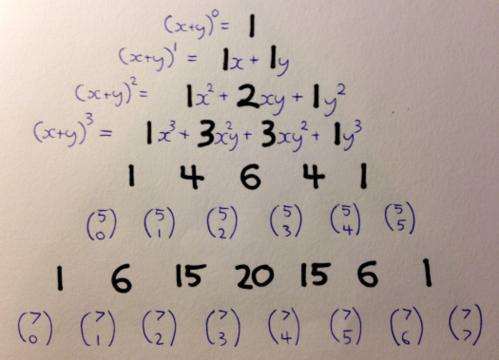
Pascal's triangle can even make some dreaded high-school algebra a lot easier.
If you find yourself in the unfortunate position of having to expand (x+y) to the power of n, you can skip straight past all the horrible working out to the answer.
Start by putting down all n of the x's multiplied together, and as you move from left to right, remove one x and replace it with a y until there are no x's left at all.
Once you add up all these terms, all that's left to do is fill in the right coefficients. This would be the hardest part of the exercise… were it not for the fact that you can read them straight off Pascal's triangle! Just go to the line that has n on the first inner diagonal, and they'll be waiting for you.
The secret to this magic shortcut is the binomial theorem for expanding brackets - together with the fact that the digits in Pascal's triangle are really combinations in disguise…
On the tenth day of Christmas, the triangle gave to me…
All the combinations
Let's briefly return to return to the historical roots of Pascal's triangle. As mentioned above, all the numbers in Pascal's triangle actually correspond to combinations – that is, they tell us exactly how many ways we can choose a small group of objects out of a larger group (if the order in which we choose things doesn't matter).
Combinations are very important to probability theorists and their gambling friends, since counting the number of ways that something can happen is the most straightforward way to determine the probability of it happening.
Combinations can be written in a variety of ways, but the most common notation is to put two numbers inside a pair of parentheses – one on top (to tell us the total number of objects) and one on the bottom number (to tell us just how many of those objects we're going to choose). And these combinations line up perfectly with Pascal's triangle – the top number matches the row of the triangle and the bottom number tells us how far along the row to go.
For instance, say we have 5 pieces of fruit and vegetables: an Apple, a Banana, a Carrot, a Durian and an Eggplant. We'd like to pick 2 of them to use in our cooking. How many possible choices can we make?
We could carefully list all the possibilities (remembering that the order doesn't matter) – then we'd have AB, AC, AD, AE, BC, BD, BE, CD, CE, DE and a total of 10 possibilities. Alternatively, we could count down 5 rows (starting from 0) and across 2 places (again starting from 0) in Pascal's triangle – and also arrive at the number 10.
On the eleventh day of Christmas, the triangle gave to me…
Powers of eleven

For a particularly cool party trick, look at what happens when you squish all the numbers in a given row together to make one large number. Actually, we do have to be a little bit careful when dealing with like double-digit numbers and the like – rather than just squishing them together, we'll move the extra digit over to the left (in a similar manner to primary school addition).
As an example, when squishing the 1-4-6-4-1 row together, we just end up with the number 14641. But when we squish the 1-5-10-10-5-1 row together, we split the 10s up into a 1 (which gets added to the number on the left) and a 0 (which stays put).
Upon splitting the first 10 this way, the row becomes 1-(5+1)-(0)-10-5-1. When the second 10 is split, the row ends up as 1-(5+1)-(0+1)-0-5-1, or 1-6-1-0-5-1, and we end up with the number 161051 (it's a lot easier to do it than to describe it, trust me!).
Just as combining the numbers in a row by adding them gives us the powers of two, combining the numbers in a row by squishing them together like this gives us the powers of eleven! Also note that 11 to the power of 0 really wants to be equal to 1 as well…
On the twelfth day of Christmas, the triangle gave to me…
Sierpinski's fractal!

Now for my all-time favourite Pascal pattern – I never cease to be amazed by how my favourite fractal triangle of all time sneakily hides itself in Pascal's triangle too.
Siepinski's triangle is the shape you get when you take an equilateral triangle, cut away the middle piece, then cut away the middle pieces from all the smaller triangles that are left over, then keep going forever (or until you get tired).
How does this relate to Pascal's triangle? Look at what happens when you shade in all the odd numbers with one colour, and all the even numbers with a different colour!
Wishing you a Merry Christmas and a Happy New Year; may your holidays be filled with fun maths and good cheer! And may your carols be henceforth untouched by mathematicians.
Source: The Conversation
This story is published courtesy of The Conversation (under Creative Commons-Attribution/No derivatives).
![]()