Forget the needle, consider the haystack: Uncovering hidden structures in massive data collections
(Phys.org) —Advances in computer storage have created collections of data so huge that researchers often have trouble uncovering critical patterns in connections among individual items, making it difficult for them to realize fully the power of computing as a research tool.
Now, computer scientists at Princeton University have developed a method that offers a solution to this data overload. Using a mathematical method that calculates the likelihood of a pattern repeating throughout a subset of data, the researchers have been able to cut dramatically the time needed to find patterns in large collections of information such as social networks. The tool allows researchers to identify quickly the connections between seemingly disparate groups such as theoretical physicists who study intermolecular forces and astrophysicists researching black holes.
"The data we are interested in are graphs of networks like friends on Facebook or lists of academic citations," said David Blei, an associate professor of computer science and co-author on the research, which was published Sept. 3 in the Proceedings of the National Academy of Science. "These are vast data sets and we want to apply sophisticated statistical models to them in order to understand various patterns."
Finding patterns in the connections among points of data can be critical for many applications. For example, checking citations to scientific papers can provide insights to the development of new fields of study or show overlap between different academic disciplines. Links between patents can map out groups that indicate new technological developments. And analysis of social networks can provide information about communities and allow predictions of future interests.
"The goal is to detect overlapping communities," Blei said. "The problem is that these data collections have gotten so big that the algorithms cannot solve the problem in a reasonable amount of time."
Currently, Blei said, many algorithms uncover hidden patterns by analyzing potential interactions between every pair of nodes (either connected or unconnected) in the entire data set; that becomes impractical for large amounts of data such as the collected citations of the U.S. Patent Office. Many are also limited to sorting data into single groups.
"In most cases, nodes belong to multiple groups," said Prem Gopalan, a doctoral student in Blei's research group and lead author of the paper. "We want to be able to reflect that."
In very basic terms, the researchers approached the problem by dividing the analysis into two broad tasks. In one, they created an algorithm that quickly analyzes a subset of a large database. The algorithm calculates the likelihood that nodes belong to various groups in the database. In the second broad task, the researchers created an adjustable matrix that accepts the analysis of the subset and assigns "weights" to each data point reflecting the likelihood that it belongs to different groups.
Blei and Gopalan designed the sampling algorithm to refine its accuracy as it samples more subsets. At the same time, the continual input from the sampling to the weighted matrix refines the accuracy of the overall analysis.
The math behind the work is complex. Essentially, the researchers used a technique called stochastic optimization, which is a method to determine a central pattern from a group of data that seem chaotic or, as mathematicians call it, "noisy." Blei likens it to finding your way from New York to Los Angeles by stopping random people and asking for directions—if you ask enough people, you will eventually find your way. The key is to know what question to ask and how to interpret the answers.
"With noisy measurements, you can still make good progress by doing it many times as long as the average gives you the correct result," he said.
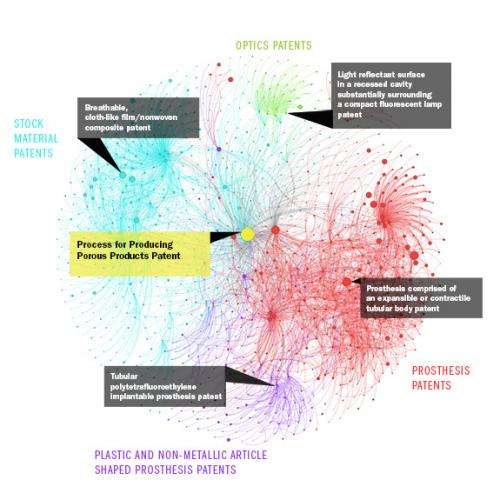
In their PNAS article, the researchers describe how they used their method to discover patterns in the connections between patents. Using public data from the U.S. National Bureau of Economic Research, Gopalan and Blei analyzed connections to the 1976 patent "Process for producing porous products."
The patent, filed by Robert W. Gore (who several years earlier discovered the process that led to the creation of the waterproof fabric Gore-Tex), described a method for producing porous material from tetrafluoroethylene polymers. The researchers analyzed a data collection of 3.7 million nodes and found that connections between Gore's 1976 filing and other patents formed 39 distinct communities in the database.
The patent "has influenced the design of many everyday materials such as waterproof laminate, adhesives, printed circuit boards, insulated conductors, dental floss and strings of musical instruments," the researchers wrote.
In the past, researchers struggled to find nuggets of critical information in data. The new challenge is not finding the needle in the data haystack, but finding the hidden patterns in the hay.
"Take the data from the world, from what you observe, and then untangle it," Blei said. "What generated it? What are the hidden structures?"
Journal information: Proceedings of the National Academy of Sciences
Provided by Princeton University