Physicists publish solution to the quantum measurement problem
(Phys.org) —Quantum mechanics is a highly successful theory, but its interpretation has still not been settled. In their recent opus magnum, Theo Nieuwenhuizen (Institute of Physics, UvA) and colleagues claim to have found a solution to the so-called quantum measurement problem.
This subject of measurement in quantum mechanics was studied by many prominent scientists, including Heisenberg, von Neumann, Wigner and van Kampen. As the only point of contact between theory and reality lies in measurements, a proper theoretical understanding of quantum measurements seems mandatory. In their 166-pages article, Nieuwenhuizen and his colleagues Armen Allahverdyan (Yerevan Physics Institute) and Roger Balian (IPhT, Saclay), take up this challenge.
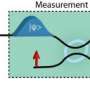
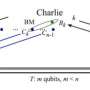
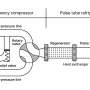
After reviewing the literature on measurement models, they focus on the so-called Curie-Weiss model for quantum measurements. The joint dynamics of the tested system coupled to the measurement apparatus now produces results that explain the measurement postulates. It shows that the off-diagonal terms ("cat-terms") disappear in a physical process due to the coupling to the apparatus, on a basis selected by the interaction Hamiltonian. The registration of the measurement outcomes by the pointer of the apparatus occurs because the measurement triggers the transition from the initial metastable state to one of the stable final states; the apparatus being large, this means an amplification of the signal. The transition of the pointer variable from its initial metastable state to one of the final stable states is a process with classical features, such as the dumping of excess free energy in the bath.
'Mathematical embarrassment'
Still, for theorists the task is not over then. It is known that due to quantum oddities, the state of the apparatus and tested system at the end of the measurement, cannot be associated with the single outcome that one observes in practice. This poses the infamous "quantum measurement problem", for which the authors seek, as they call it, "a physical way out of a mathematical embarrassment". They find an answer in subtle dynamical instabilities inside the apparatus near the end of the measurement. The only stable states are the ones known from the measurement postulates. Hence only these are relevant, which leads to ordinary probabilities, that can be connected to individual measurements.
Altogether, nothing else than standard quantum theory appears required for understanding ideal measurements. The quantum physics postulates of textbooks, the collapse of the wave packet and the registration with Born probabilities, derive from the quantum rules themselves, so in essence they are not needed. The statistical formulation of quantum mechanics, though abstract and minimalist, is sufficient to explain all relevant features. Since alternative interpretations involve unnecessary assumptions of one kind or another, the authors advocate the usage of the statistical formulation in physics education of quantum mechanics.
More information: Physics Reports (2013), 525, 1, 1–166. www.sciencedirect.com/science/ … ii/S0370157312004085
Provided by University of Amsterdam