Uncertainty revisited: Novel tradeoffs in quantum measurement

(Phys.org) —There is, so to speak, uncertainty about uncertainty – that is, over the interpretation of how Heisenberg's uncertainty principle describes the extent of disturbance to one observable when measuring another. More specifically, the confusion is between the fact that, as Heisenberg first intuited, the measurement of one observable on a quantum state necessarily disturbs another incompatible observable, and the fact that on the other hand the indeterminacy of the outcomes when either one or the other observable is measured is bounded. Recently, Dr. Cyril Branciard at The University of Queensland precisely quantified the former by showing how it is possible to approximate the joint measurement of two observables, albeit with the introduction of errors with respect to the ideal measurement of each. Moreover, the scientist characterized the disturbance of an observable induced by the approximate measurement of another one, and derived a stronger error-disturbance relation for this scenario.

Dr. Branciard describes the research and challenges he encountered. "Quantum theory tells us that certain measurements are incompatible and cannot be performed jointly," Branciard tells Phys.org. For example, he illustrates, it is impossible to simultaneously measure the position and speed of a quantum particle, the spin of a particle in different directions, or the polarization of a photon in different directions.

"Although such joint measurements are forbidden," Branciard continues, "one can still try to approximate them. For instance, one can approximate the joint measurement of the spin of a particle in two different directions by actually measuring the spin in a direction in between. At the price of accepting some errors; this yields partial information on the spin in both directions – and the larger the precision is on one direction, the larger the error on the other must be." While it's challenging to picture what it means to measure a property "in between position and speed," he adds, it's possible to measure something that will give partial information on both the position and speed – but again, the more precise the position is measured, the less precise the speed, and vice versa.

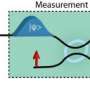
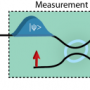
There is therefore a tradeoff between precision achievable for each incompatible observable, or equivalently on the errors made in their approximations. What exactly is this tradeoff? How well can one approximate the joint measurement? What fundamental limits does quantum theory precisely impose? This tradeoff – between the error on one observable versus the error on the other – can be characterized by so-called error-tradeoff relations, which show that certain values of errors for each observable are forbidden.

"Certain error-tradeoff relations were known already, and set bounds on the values allowed," Branciard explains. "However, it turns out that in general those bounds could not be reached, since quantum theory actually restricts the possible error values more than what the previous relations were imposing." In his paper, Branciard derives new error-tradeoff relations which are tight, in the sense that the bounds they impose can be reached when one chooses a "good enough" approximation strategy. He notes that they thus characterize the optimal tradeoff one can have between the errors on the two observables.

Branciard points out that the fact that the joint measurement of incompatible observables is impossible was first realized by Heisenberg in 1927, when, in his seminal paper, he explained that the measurement of one observable necessarily disturbs the other, and suggested an error-disturbance relation to quantify that. "General uncertainty relations were soon to be derived rigorously," Branciard continues.

More specifically, the uncertainty relation known as the uncertainty principle or Heisenberg principle is a mathematical inequality asserting that there is a fundamental limit to the precision with which certain pairs of physical properties of a particle known as complementary variables, such as a particle's position and momentum, can be known simultaneously. In the case of position and momentum, the more precisely the position of a particle is determined, the less precisely its momentum can be known, and vice versa.

"However," Branciard notes, these "standard" uncertainty relations quantify a different aspect of Heisenberg's uncertainty principle: Instead of referring to the joint measurement of two observables on the same physical system – or to the measurement of one observable that perturbs the subsequent measurement of the other observable on the same system, as initially considered by Heisenberg – standard uncertainty relations bound the statistical indeterminacy of the measurement outcomes when either one or the other observable is measured on independent, identically prepared systems."

Branciard acknowledges that there has been, and still is, confusion between those two versions of the uncertainty principle – that is, the joint measurement aspect and the statistical indeterminacy for exclusive measurements – and many physicists misunderstood the standard uncertainty relations as implying limits on the joint measurability of incompatible observables. "In fact," he points out, "it was widely believed that the standard uncertainty relation was also valid for approximate joint measurements, if one simply replaces the uncertainties with the errors for the position and momentum. However, this relation is in fact in general not valid."

Surprisingly little work has been done on the joint measurement aspect of the uncertainty principle, and it has been quantified only in the last decade when Ozawa¹ derived the first universally valid trade-off relations between errors and disturbance – that is, valid for all approximation strategies for the joint measurement error-tradeoff relations for joint measurements. "However," says Branciard, "these relations were not tight. My paper presents new, stronger relations that are. In order to quantify the uncertainty principle for approximate joint measurements and derive error-tradeoff relations," he adds, "one first needs to agree on a framework and on definitions for the errors in the approximation. Ozawa developed such a framework for that, on which I based my analysis."

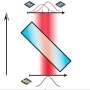
A key aspect in Branciard's research is that quantum theory describes the states of a quantum system, their evolution and measurements in geometric terms – that is, physical states are vectors in a high-dimensional, complex Hilbert space, and measurements are represented by projections onto certain orthogonal bases of this high-dimensional space. "I made the most of this geometric picture to derive my new relations," Branciard explains. "Namely, I represented ideal and approximate measurements by vectors in a similar (but real) space, and translated the errors in the approximations into distances between the vectors. The incompatibility of the two observables to be approximated gave constraints on the possible configuration of those vectors in terms of the angles between the vectors." By then looking for general constraints on real vectors in a large-dimensional space, and on how close they can be from one another when some of their angles are fixed, Branciard was able to derive his relation between the errors in the approximate joint measurement.

Branciard again notes that he used the framework developed mainly by Ozawa, who proposed to quantify the errors in the approximations by the statistical deviations between the approximations and their ideal measurements. In this framework, any measurement can be used to approximate any other measurement, in that the statistical deviation defines the error. However, the advantage of Branciard's new relation over previously derived ones is that it is, as he described it above, tight. "It does not only tell that certain values are forbidden," he points out, "but also shows that the bounds they impose can be reached. In fact," he illustrates, "I could show how to saturate my new relation for any pair of observables A and B and for any quantum state, and reach all optimal error values eA and eB, whether one wants a small eA at the price of having to increase eB, or vice versa."

Moreover, he continues, the fact that it is tight is relevant experimentally, if one aims at testing these kinds of relations. "Showing that a given relation is satisfied is trivial if the relation is universally valid, since any measurement should satisfy it. What is less trivial is to show experimentally that one can indeed reach the bound of a tight relation. Experimental techniques now allow one to perform measurements down to the limits imposed by quantum theory, which makes the study of error-tradeoff relations quite timely. Also," he adds, "the tightness of error-tradeoff relations may be crucial if one considers applications such as the security of quantum communications: If one uses such relations to study how quantum theory restricts the possible actions of an eavesdropper, it will not be enough to say what cannot be done using simply a valid relation, but also what can be done when quantified by a tight relation."

In Branciard's framework, the error-disturbance scenario initially considered by Heisenberg can be seen as a particular case of the joint measurement scenario, in that an approximate measurement of the first observable and a subsequent measurement of the then-disturbed incompatible second observable, taken together, constitute an approximate measurement of both observables. More specifically, the second measurement is only approximated because it is performed on the system after it has been disturbed by the first measurement.

"Hence, in my framework," Branciard summarizes, "any constraint on approximation errors in joint measurements also applies to the error-disturbance scenario, in which the error on the second observable is interpreted as its disturbance and error-tradeoff relations simply imply error-disturbance relations. In fact," he adds, "while the error-disturbance case is a particular case of the more general joint measurement scenario, it's actually more constrained. This is because in that scenario the approximation of the second observable is done via the actual measurement of precisely that observable after the system has been disturbed by the approximate measurement of the first observable." This restricts the possible strategies for approximating a joint measurement, and as a consequence stronger constraints can generally be derived for errors versus disturbances rather than for error tradeoffs.

Branciard gives a specific example. "Suppose the second observable can produce two possible measurement results – for example, +1 or -1 – that could correspond to measuring spin or polarization in a given direction. In the error-disturbance scenario, the approximation of the 2nd observable – that is, the actual measurement of that observable on the disturbed system – is restricted to produce either the result +1 or the result -1. However, in a more general scenario of approximate joint measurements, it may give lower errors in my framework to approximate the measurement by outputting other measurement results, say 1/2 or -3. For these reasons, one can in general actually derive error-disturbance relations that are stronger than error-tradeoff relations, as shown in my paper."

The uncertainty principle is one of the main tenets of quantum theory, and is a crucial feature for applications in quantum information science, such as quantum computing, quantum communications, quantum cryptography, and quantum key distribution. "Standard uncertainty relations in terms of statistical indeterminacy for exclusive measurements are already used to prove the security of quantum key distribution," Branciard points out. "In a similar spirit, it may also be possible to use the joint measurement version of the uncertainty principle to analyze the possibility for quantum information applications. This would, however, probably require the expression of error-tradeoff relations in terms of information, by quantifying the limited information gained on each observable, rather than talking about errors."

Looking ahead, Branciard describes possible directions for future research. "As mentioned, in order to make the most of the joint measurement version of the uncertainty principle and be able to use it to prove, for instance, the security of quantum information applications, it would be useful to express it in terms of information-theoretic – that is, entropic – quantities. Little has been studied in this direction, which would require developing a general framework to correctly quantify the partial information gained in approximate joint measurements, and then derive entropic uncertainty relations adapted to the scenarios under consideration."

Beyond its possible applications for quantum information science, Branciard adds, the study of the uncertainty principle brings new insights on the foundations of quantum theory – and for Branciard, some puzzling questions in quantum foundations include why does quantum theory impose such limits on measurements, and why does it contain so many counterintuitive features, such as quantum entanglement and non locality?

"A link has recently been established between standard uncertainty relations and the nonlocality of any theory. Studying this joint measurement aspect of the uncertainty principle," Branciard concludes, "may bring new insights and give a more complete picture of quantum theory by offering to address these metaphysical questions – which have been challenging physicists and philosophers since the invention of quantum theory – from a new perspective."

© 2013 Phys.org. All rights reserved.