The changing phase of quantum materials: Theoretical model could aid search for ideal material for quantum computers

Matter is categorized as either conductive, semi-conductive or resistive to the flow of electrons based on its bulk properties. However, physicists have now predicted a new state of matter in which the bulk of the material is insulating—resisting electron flow—but where electrons are free to move along its edges. The possibility of such a material, known as a 'topological insulator', has caused a great deal of excitement among physicists because its surface conducting states are unusually stable, making them a promising resource for use in quantum computers. Bohm-Jung Yang and Naoto Nagaosa from the RIKEN Center for Emergent Matter Science and their co‐workers have now devised a general theory for how an insulator changes into a topological insulator, which should aid in the practical search for such materials.
A full understanding of a material requires knowledge of how its properties vary as the external environment changes. Increasing the pressure of a gas, for example, can change it to a liquid, and higher pressures cause its atoms to bond together to form a solid crystal. Such changes of state at temperatures near absolute zero are known as quantum phase transitions. The theoretical model developed by Nagaosa's team describes quantum phase transitions involving topological insulator states.
"We want to understand how two insulating phases with distinct topological properties can be transformed from one to the other when external perturbations are applied," explains Nagaosa. "Our theory shows the importance of atomic symmetry in understanding this topological phase transition."
A topological quantum phase transition was recently experimentally observed in bismuth thallium sulfide selenide, a compound with an 'inversion symmetric' atomic arrangement—a structure that looks the same when reflected with respect to a point. The model put forward by Nagaosa and his colleagues goes beyond such materials by understanding phase transitions in 'noncentrosymmetric' materials, which do not exhibit this simplifying property.
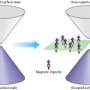
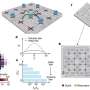
The researchers' sophisticated model predicts that three-dimensional noncentrosymmetric materials can either change directly from a conventional insulator to a topological insulating state, or pass through an intermediate semi-metal state (Fig. 1). Their model provides detailed estimates for the temperature dependence of many of the properties of this semi-metallic phase, and the conditions required for a phase transition, known as quantum critical points. "The unique physical properties of the semi-metallic state that we have identified will provide a useful guideline for experimental proof of a topological phase transition in three-dimensional noncentrosymmetric systems," says Nagaosa.
More information: Yang, B. et al. Theory of topological quantum phase transitions in 3D noncentrosymmetric systems. Physical Review Letters 110, 086402 (2013). dx.doi.org/10.1103/PhysRevLett.110.086402
Journal information: Physical Review Letters
Provided by RIKEN