March 26, 2013 report
Researchers develop quantum computer algorithm for counting prime numbers
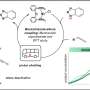
![Structure of the Quantum Primality Oracle based on the Miller-Rabin primality test. A series of unitary modules implement a quantum version of the modular exponentiation tests required by the classical test. The total number of tests m is smaller than n2. Credit: arXiv:1302.6245 [quant-ph] Researchers develop quantum computer algorithm for counting prime numbers](https://scx1.b-cdn.net/csz/news/800a/2013/56tyfyg.jpg)
(Phys.org) —Two math and physics researchers from the University's of Barcelona and Madrid respectively have developed an algorithm to count prime numbers using a quantum computer. José Latorre and Germán Sierra describe in their paper they've uploaded to the preprint server arXiv, their formula that uses spin states of quantum bits (qubits) to calculate the number of prime numbers below a given value.
Prime numbers are natural numbers that can only be divided evenly by themselves or 1—mathematcians have been wrestling since the time of Euclid to come up with a way to identify them, all to no avail. The only way to find one currently is to pick a number and see if it can be divided evenly. Because of that, few prime numbers were found until the advent of computers. Now, big computers can be run for months at a time to determine the next prime number past the one that is known.
In 1859, mathematician Bernhard Riemann came up with a formula that can be used to ascertain, given a single number, how many prime numbers fall below it. The problem here however, is no one has been able to prove whether it is correct or not. Because it can't be proved true, researchers have been trying to prove it false by giving it numbers where all the primes below it have been identified. Thus far, such attempts have reached a number as high as 1024. Running the algorithm on a regular computer takes enormous amounts of time—trying X=1025, for example would likely take about nine months. In this new effort, the research duo from Spain has come up with an algorithm for doing the job on a quantum computer that takes advantage of the spin states of qubits.
The algorithm can't be run just yet however, because a quantum computer running it would have to be able to manipulate 80 qubits at a time, which is far bigger than anything that has been built thus far. Because quantum computers are still in their infancy, their designs are still taking shape, and because of that it's impossible to say for sure just how much faster such a computer could calculate Riemann's formula, but most would likely agree that the difference would be significant.
More information: Quantum Computation of Prime Number Functions, arXiv:1302.6245 [quant-ph] arxiv.org/abs/1302.6245
Abstract
We propose a quantum circuit that creates a pure state corresponding to the quantum superposition of all prime numbers less than 2^n, where n is the number of qubits of the register. This Prime state can be built using Grover's algorithm, whose oracle is a quantum implementation of the classical Miller-Rabin primality test. The Prime state is highly entangled, and its entanglement measures encode number theoretical functions such as the distribution of twin primes or the Chebyshev bias. This algorithm can be further combined with the quantum Fourier transform to yield an estimate of the prime counting function, more efficiently than any classical algorithm and with an error below the bound that allows for the verification of the Riemann hypothesis. Arithmetic properties of prime numbers are then, in principle, amenable to experimental verifications on quantum systems.
via Newscientist
Journal information: arXiv
© 2013 Phys.org