September 10, 2012 report
Statisticians try to calculate probability of another 9/11 sized attack
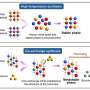
![(upper) Number of deadly (domestic and international) terrorist events worldwide for the ten year period 1998–2007, and three forecast scenarios. (lower) Fraction of events that are severe, killing at least 10 individuals and its 10-year average (dashed line). Credit: arXiv:1209.0089v1 [physics.data-an] Statisticians try to calculate probability of another 9/11 sized attack](https://scx1.b-cdn.net/csz/news/800a/2012/drgererr.jpg)
(Phys.org)—In the world of probability and statistics almost anything can be labeled as a percentage of likelihood of occurring; statistics based on actual numbers give rise to probabilistic estimates that in some cases may be very accurate, not so accurate, or impossible to prove one way or another. With such a view, two statisticians, Aaron Clauset and Ryan Woodard have trained their sights on terrorist incidents and the likelihood of them occurring, specifically, the big kinds, like 9/11. They have found, as they describe in their paper they've uploaded to the preprint server arXiv, that using tried and true statistical models, that the likelihood of another attack as big, or even bigger, than 9/11, is as likely as not.
The basis of any statistical model is data and in this case the data was based on the number of terrorist acts committed between the years 1969 and 2007, which of course included 9/11. The attack on the twin towers in New York stands out of course, as the number of people killed that day was six times more than any other terrorist attack. To first see how accurate any given model might be, the researchers calculated the likelihood of 9/11 actually happening based on prior data using three different types of standard models; power law, exponential distributions and log-normal. After crunching the numbers they say it came down to between an eleven to thirty five percent chance, which they say is reasonable and shows that what happened on 9/11 was not unlikely, statistically speaking, to have happened.
The two then applied the same models looking forward into the future and came up with a likelihood of another 9/11 type attack falling between twenty and fifty percent, depending on which model was used and assuming that things remain the same, i.e. the average number of attacks per year (approximately 2000) stays the same. But, realizing that the odds of things holding steady isn't itself very realistic they also tried factoring in such destabilizing scenarios as rising food prices or things calming or growing worse in two of the current hot spots for terrorism; Iraq and Afghanistan. In such cases the models became truly alarming, indicating that in the worst case scenarios the likelihood of another event as deadly as 9/11 occurring, becomes nearly ninety five percent.
More information: Estimating the historical and future probabilities of large terrorist events, arXiv:1209.0089v1 [physics.data-an] arxiv.org/abs/1209.0089
Abstract
Quantities with right-skewed distributions are ubiquitous in complex social systems, including political conflict, economics and social networks, and these systems sometimes produce extremely large events. For instance, the 9/11 terrorist events produced nearly 3000 fatalities, nearly six times more than the next largest event. But, was this enormous loss of life statistically unlikely given modern terrorism's historical record? Accurately estimating the probability of such an event is complicated by the large fluctuations in the empirical distribution's upper tail. We present a generic statistical algorithm for making such estimates, which combines semi-parametric models of tail behavior and a non-parametric bootstrap. Applied to a global database of terrorist events, we estimate the worldwide historical probability of observing at least one 9/11-sized or larger event since 1968 to be 11-35%. These results are robust to conditioning on global variations in economic development, domestic versus international events, the type of weapon used and a truncated history that stops at 1998. We then use this procedure to make a data-driven statistical forecast of at least one similar event over the next decade.
Journal information: arXiv
© 2012 Phys.org