Is a classical electrodynamics law incompatible with special relativity?

(Phys.org) -- The laws of classical electromagnetism that were developed in the 19^th century are the same laws that scientists use today. They include Maxwell’s four equations along with the Lorentz law, which describes the force exerted by electric and magnetic fields on charged particles. But Masud Mansuripur, a professor of Optical Sciences at The University of Arizona in Tucson, is now arguing that the Lorentz law of force is incompatible with special relativity and momentum conservation, and should be abandoned. In a recent issue of Physical Review Letters, he has suggested replacing the Lorentz law with a more general expression of electromagnetic force density, such as one developed by Albert Einstein and Jakob Laub in 1908.

However, Mansuripur’s bold claim of a paradox with the Lorentz law has generated some intense criticism. One critic, Daniel Vanzella, a physics professor at the University of Sao Paulo in Sao Carlos, Brazil, has submitted a comment to Physical Review Letters arguing that the Lorentz law is perfectly compatible with special relativity, and that Mansuripur has misunderstood relativistic mechanics. The only paradox, Vanzella says, is why the high-ranking journal accepted the paper in the first place.

Charge-magnet paradox

The basis of Mansuripur’s argument is that the Lorentz law violates special relativity by producing different results in different reference frames. According to special relativity, the laws of physics – including electromagnetism – must be the same in all non-accelerating reference frames.

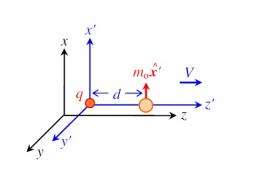
He describes a scenario in which a magnetic dipole and a nearby electric charge are located a certain distance apart. When the magnet and the electric charge are at rest, no net force is exchanged between the two. This is because static electric charges only produce electric fields (to which the magnet is oblivious), and static magnets only produce magnetic fields (to which the static electric charge is oblivious). Both the Lorentz law and the Einstein-Laub version give the same result: the magnet experiences neither a force nor a torque from the electric charge.

However, the Lorentz law gives a different result when a stationary observer watches the magnet and electric charge in a moving reference frame. Here, the observer sees the moving electric charge exert a torque on the moving magnet, causing the magnet to rotate as it tries to align itself with the electric field. The presence of this torque differs from the observation in the stationary reference frame where there is no torque.

On the other hand, the Einstein-Laub formula, when combined with a corresponding torque formula, gives zero torque value for observers in both reference frames, complying with special relativity.

The Lorentz law’s incompatibility with special relativity is not its only shortcoming, according to Mansuripur. Another equally important issue is the long-standing problem of “hidden momentum,” in which he shows that the Lorentz law fails to conserve momentum in certain situations involving magnetic media. In contrast, the Einstein-Laub equations show complete consistency with the conservation laws. For Mansuripur, this evidence indicates that the Einstein-Laub formula should be considered as a better way to understand classical electrodynamics.

“This work provides a firm basis for all calculations of force, torque, momentum and angular momentum whenever electromagnetic fields (microwave, light, etc.) interact with material media,” Mansuripur told Phys.org. “The electromagnetic momentum and angular momentum become well-defined universal entities (i.e., the Abraham momentum), the need for ‘hidden momentum’ disappears, and satisfaction of conservation laws as well as conformity with special relativity are guaranteed.

He explains that, during the past century, there has been a proliferation of equations for force and torque in the scientific literature, with scientists using several different formulas for the electromagnetic momentum.

“My paper fixes the foundational equations and allows researchers to compare their experimental results against a single, well-defined theory,” he said.

Quantum nature

According to Mansuripur, the underlying reason for the difference between the Lorentz law and Einstein-Laub formula involves how each equation mathematically describes the quantum nature of electromagnetic fields and media.

For its part, the Lorentz law depicts electric and magnetic dipoles as pairs of positive and negative charges or stable loops of current that interact with electromagnetic fields in terms of free and bound charges and currents. In contrast, the Einstein-Laub formula describes material media as spatio-temporal distributions of charge, current, polarization, and magnetization. Mansuripur explains why this distinction is important.

“The fact that the electron orbits inside atoms and molecules are stable is a quantum-mechanical phenomenon,” he said. “Neither Maxwell’s equations nor the Lorentz law of force (and nor, for that matter, the Einstein-Laub force/torque equations) can account for the stability of the electron orbit. The fact that electrons, protons and neutrons have a magnetic moment associated with their spin angular momentum is also a relativistic quantum effect that has no explanation within classical physics. What Maxwell’s equations and the Lorentz law (or the Einstein-Laub law) do is provide formulas that describe the behavior of fields and material media as they are, without attempting to justify that behavior. The Lorentz law, however, simplifies the underlying physics by assuming that electric and magnetic dipoles can be treated as distributions of ordinary electrical charge and current. In contrast, the Einstein-Laub equation and the accompanying torque equation treat free charge, free current, electric dipoles, and magnetic dipoles as four distinct constituents of material media.

“So, for example, the fact that a magnetic dipole is associated with something resembling a loop of current is a quantum mechanical effect. The Lorentz law does not ignore this fact, but it takes the resemblance to a current loop too far, treating the magnetic dipole as if it were actually a loop of ordinary current. In contrast, the Einstein-Laub formula acknowledges that magnetic dipoles exist as distinct entities – what makes them distinct is quantum mechanics, of course, but Einstein-Laub does not attempt to justify the existence of these dipoles or their nature. The Einstein-Laub formulas then provide a ‘recipe’ for calculating the force and torque on these dipoles, which turns out to be different from the ‘recipe’ provided by the Lorentz law.”

No paradox?

One critic of Mansuripur’s ideas, Vanzella, thinks that the paper is so flawed that it should not have been published at all. In his comment submitted to the journal, Vanzella points out that the Lorentz force can be put in a covariant form. In special relativity, a covariant law cannot lead to incompatible descriptions of the same phenomenon in different inertial reference frames. He explains that Mansuripur has incorrectly used relativistic mechanics and ignored a hidden momentum that makes the Lorentz formula predict a torque in one reference frame but not another.

“This has blown way out of proportion,” Vanzella said. “Let me begin by stating the most important point: there is no incompatibility between the Lorentz force and special relativity. This is not a matter of opinion: any relativist knows that this is impossible for any specially-covariant law (as is the Lorentz force). By construction, a specially-covariant law is compatible with special relativity. This means that if it leads to a satisfactory description of a phenomenon in one inertial frame, then it leads to consistent descriptions in any inertial frame; there are no paradoxes.”

He added that apparent paradoxes appear frequently when dealing with special relativity, but these paradoxes are actually due to simply missing or overlooking part of the relativistic argument. He says that a very similar “paradox” to the charge-magnet paradox, called the Trouton-Noble paradox, was presented and resolved more than 100 years ago.

"In this particular case, using a current loop in a perfectly-conducting ring to model the magnet's magnetic moment, one has to use special relativity to show that, even when the ring is at rest, the total momentum of the system is not zero (when subject to an external electric field),” he explained. “This momentum has been termed ‘hidden’ in the literature and this has led to some confusion, but let me stress that it is real momentum. Mansuripur is missing the point that this momentum is not an ad hoc invention only to solve paradoxes; its existence is forced upon us (upon Nature, actually) due to the principles of special relativity alone. In my comment I do not postulate the existence of this momentum. I simply use special relativity to calculate it; no additional hypothesis other than special relativity and the Lorentz force. Therefore, when Mansuripur dismisses this ‘hidden’ momentum he is doing exactly what I said is needed to arrive at a paradox: missing or overlooking part of the relativistic argument.”

Despite his strong disagreement with Mansuripur, he emphasized that his criticism does not suggest anything against Mansuripur’s scientific credibility.

“Please note that I don't think that Mansuripur not knowing the solution of the ‘charge-magnet paradox’ (or not understanding the given solution) is that bad,” Vanzella said. “Special relativity is certainly not his expertise and confuses a lot of people, even physicists.”

He also added that he’s not necessarily arguing that the Lorentz law must be the correct law of force, either, but just that special relativity cannot be used to testify against it. The question of which law is correct is an experimental issue. Still, he’s adamant that there is no paradox in this situation.

“I wouldn't even call Mansuripur's idea ‘controversial,’” he said. “Would you call ‘controversial’ the idea that the Earth is flat? It is simply and provably wrong (I mean the claim that the Lorentz force is incompatible with special relativity).”

In a response to Vanzella’s comment, also submitted to Physical Review Letters, Mansuripur has stuck to his original argument, explaining that there is no need to introduce hidden momentum, and that the Trouton-Noble paradox was subtly but significantly different than the charge-magnet paradox.

Future of Einstein-Laub

Despite the advantages of Einstein-Laub formula, Mansuripur acknowledges that it is not without its own problems. In 1979, physicist Iver Brevik performed an extensive review of the Einstein-Laub formula and other possible candidates for an energy-momentum tensor for the electromagnetic field. In some of the experiments, the Einstein-Laub formula did not match actual observations as closely as another formula, the Helmholtz force equation. However, Mansuripur argues that, due to the potential significance of this idea, the contrary evidence deserves a closer examination.

“My colleagues and I are currently trying to identify situations where the distinction between the Lorentz law and the Einstein-Laub formulation is unambiguous, then try to conduct experiments to determine which law is operative in such situations,” he said. “Personally, I don’t attach much significance to the historical evidence against the Einstein-Laub formulation as reviewed in the paper by Brevik. The experiments were all electrostatic experiments, involving the flow of some dielectric fluid into a capacitor. The theoretical methods used to analyze the problem were extremely confusing; many approximations were made, and the Einstein-Laub formula itself was never used directly; instead they used a stress tensor associated with Einstein-Laub, which I have shown elsewhere to be incorrect.

Mansuripur also plans to further investigate what he thinks has been a much overlooked distinction between the two formulas: a term that describes the force density of an electric field acting on the polarization density of a material medium. Whereas the Lorentz law uses –(del.P)E, the Einstein-Laub formula uses (P.del)E. Although the two formulations give exactly the same total force and total torque on any solid object, differences emerge when dealing with soft objects.

“If applied to soft objects such as biological cells under intense illumination or droplets of oil or water in optical tweezers, the two formulas give different force and torque ‘distributions’ throughout the object,” he said. “This difference in force/torque distribution will then manifest itself in different deformations of the object under intense illumination. Our near-term goal, therefore, is to look for deformations of soft objects in optical tweezers experiments. A long-term goal is to look for observable differences between Lorentz and Einstein-Laub in magnetic materials.”

Copyright 2012 Phys.org
All rights reserved. This material may not be published, broadcast, rewritten or redistributed in whole or part without the express written permission of PhysOrg.com.