Researchers find best routes to self-assembling 3-D shapes
Material chemists and engineers would love to figure out how to create self-assembling shells, containers or structures that could be used as tiny drug-carrying containers or to build 3-D sensors and electronic devices.
There have been some successes with simple 3-D shapes such as cubes, but the list of possible starting points that could yield the ideal self-assembly for more complex geometric configurations gets long fast. For example, while there are 11 2-D arrangements for a cube, there are 43,380 for a dodecahedron (12 equal pentagonal faces). Creating a truncated octahedron (14 total faces – six squares and eight hexagons) has 2.3 million possibilities.
"The issue is that one runs into a combinatorial explosion," said Govind Menon, associate professor of applied mathematics at Brown University. "How do we search efficiently for the best solution within such a large dataset? This is where math can contribute to the problem."
In a paper published in the Proceedings of National Academy of Sciences, researchers from Brown and Johns Hopkins University determined the best 2-D arrangements, called planar nets, to create self-folding polyhedra with dimensions of a few hundred microns, the size of a small dust particle. The strength of the analysis lies in the combination of theory and experiment. The team at Brown devised algorithms to cut through the myriad possibilities and identify the best planar nets to yield the self-folding 3-D structures. Researchers at Johns Hopkins then confirmed the nets' design principles with experiments.
"Using a combination of theory and experiments, we uncovered design principles for optimum nets which self-assemble with high yields," said David Gracias, associate professor in of chemical and biomolecular engineering at Johns Hopkins and a co-corresponding author on the paper. "In doing so, we uncovered striking geometric analogies between natural assembly of proteins and viruses and these polyhedra, which could provide insight into naturally occurring self-assembling processes and is a step toward the development of self-assembly as a viable manufacturing paradigm."
"This is about creating basic tools in nanotechnology," said Menon, co-corresponding author on the paper. "It's important to explore what shapes you can build. The bigger your toolbox, the better off you are."
While the approach has been used elsewhere to create smaller particles at the nanoscale, the researchers at Brown and Johns Hopkins used larger sizes to better understand the principles that govern self-folding polyhedra.
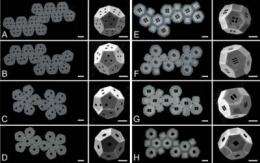
The researchers sought to figure out how to self-assemble structures that resemble the protein shells viruses use to protect their genetic material. As it turns out, the shells used by many viruses are shaped like dodecahedra (a simplified version of a geodesic dome like the Epcot Center at Disney World). But even a dodecahedron can be cut into 43,380 planar nets. The trick is to find the nets that yield the best self-assembly. Menon, with the help of Brown undergraduate students Margaret Ewing and Andrew "Drew" Kunas, sought to winnow the possibilities. The group built models and developed a computer code to seek out the optimal nets, finding just six that seemed to fit the algorithmic bill.
The students got acquainted with their assignment by playing with a set of children's toys in various geometric shapes. They progressed quickly into more serious analysis. "We started randomly generating nets, trying to get all of them. It was like going fishing in a lake and trying to count all the species of fish," said Kunas, whose concentration is in applied mathematics. After tabulating the nets and establishing metrics for the most successful folding maneuvers, "we got lists of nets with the best radius of gyration and vertex connections, discovering which nets would be the best for production for the icosahedron, dodecahedron, and truncated octahedron for the first time."
Gracias and colleagues at Johns Hopkins, who have been working with self-assembling structures for years, tested the configurations from the Brown researchers. The nets are nickel plates with hinges that have been soldered together in various 2-D arrangements. Using the options presented by the Brown researchers, the Johns Hopkins's group heated the nets to around 360 degrees Fahrenheit, the point at which surface tension between the solder and the nickel plate causes the hinges to fold upward, rotate and eventually form a polyhedron. "Quite remarkably, just on heating, these planar nets fold up and seal themselves into these complex 3-D geometries with specific fold angles," Gracias said.
"What's amazing is we have no control over the sequence of folds, but it still works," Menon added.
Provided by Brown University