Mathematics: Mapping a fixed point
(PhysOrg.com) -- For fifty years, mathematicians have grappled with a so-called “fixed point” theorem. An EPFL-based team has now found an elegant, one-page solution that opens up new perspectives in physics and economics.
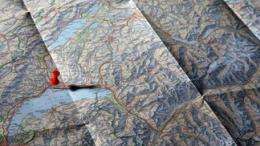
Take a map of the world. Now put it down on the ground in Central Park, against a rock on Mount Everest, or on your kitchen table; there will always be a point on the map that sits exactly on the actual physical place it represents. Obvious? Not for mathematicians. A more complex theorem, called a “fixed point theorem,” has eluded them since 1963. “Some ideas seem evident to the human mind, but in reality involve complicated concepts that are difficult to demonstrate mathematically,” says Nicolas Monod, head of EPFL’s Chair of Ergodic and Geometric Group Theory. It turns out that the answer was there all along, simple and elegant. To reach it, the team of mathematicians had take a different approach to the problem. Their discovery will impress their fellow mathematicians, of course; but on the longer term, it also will be of interest to physicists and economists.
Surprisingly, this theorem works for all kinds of maps, from a diagram of a metro route to a map of spaces used in quantum physics. But to prove it, a fixed point must be found for every possible case. Since the number of possible maps is infinite, the mathematicians were looking for a universal, purely mathematical method -- one that would work in any situation.
The challenge for the mathematicians was to find that fixed point. It was a bit like designing a method that could pinpoint the center of gravity of any object, real or purely mathematical. It seemed like an impossible task for the specialists. “That’s why this approach hadn’t been more fully explored,” Monod explains. “It was in thinking about another space and exchanging our ideas that we realized that we actually could find that center of gravity.” It was possible to determine it in a parallel space. The center of gravity was definitely there ... but outside the space you started from. It was a counterintuitive result, but one that allowed them to prove the theorem.
In 2008, a thirty-page article, full of technical jargon, almost arrived at a proof. Even Barry Edward Johnson, who formulated the theorem and worked hard to find a proof all the way up to his death in 2002, was ultimately unsuccessful. Today, the proof is only a few pages long. In addition to the indisputable intellectual satisfaction this elegant result represents, it also opens up long-term perspectives in other disciplines; theories in physics and economics, for example, both make use of the idea of fixed points.
More information: A fixed point theorem for L1 spaces, U. Bader, T. Gelander, N. Monod, Inventiones Mathematicae, 28 October 2011. dx.doi.org/10.1007/s00222-011-0363-2
Provided by Ecole Polytechnique Federale de Lausanne