Princeton researchers solve problem filling space -- without cubes

(PhysOrg.com) -- Whether packing oranges into a crate, fitting molecules into a human cell or getting data onto a compact disc, wasted space is usually not a good thing.
Now, in findings published June 20 in the Proceedings of the National Academy Sciences, Princeton University chemist Salvatore Torquato and colleagues have solved a conundrum that has baffled mathematical minds since ancient times -- how to fill three-dimensional space with multi-sided objects other than cubes without having any gaps.
The discovery could lead to scientists finding new materials and could lead to advances in communications systems and computer security.
"You know you can fill space with cubes," Torquato said, "We were looking for another way." In the article "New Family of Tilings of Three-Dimensional Euclidean Space by Tetrahedra and Octahedra," he and his team show they have solved the problem.
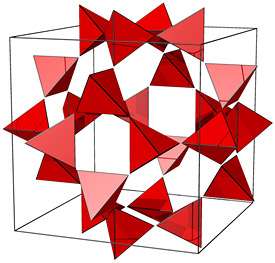
Torquato, who is a professor in the Department of Chemistry, Princeton Institute for the Science and Technology of Materials and Princeton Center for Theoretical Science, worked with Yang Jiao, a postdoctoral associate at Princeton, and John Conway, Princeton's John Von Neumann Professor in Applied and Computational Mathematics, to find that three-dimensional space can be efficiently filled with units consisting of an octahedron and six smaller tetrahedra. Moreover, the resulting patterns can be repeated infinitely.
The researchers' work involves "tiling," also known as "tessellation" after the Latin word "tessella," meaning a small cube or tile. Just as someone tiling a floor repeats a geometric pattern to fill the length and width of the floor space, Torquato and colleagues take that task to a third dimension, adding height and filling the whole room. That process involves fitting more complex three-dimensional "tiles" together, in this case the regular octahedron (a solid figure with eight triangular faces) and the regular tetrahedron (a figure with four triangular faces).
"The cube is one of five Platonic solids," Torquato explained. "It is known that the other four Platonic solids (tetrahedron, octahedron, the 12-sided dodecahedron and 20-sided icosehedron) individually cannot tile 3D space. However, we've discovered new ways to combine tetrahedra and octahedra to tile 3D space."
The phenomenon of tiling occurs in nature -- in structures within certain living cells, in the formation of crystals, and even the honeycombs in a beehive or the repeated densely packed structures in the center of a daisy, Torquato said.
"With a greater understanding of tilings, scientists can devise better and more realistic models for structures of matter; architects can come up with designs that balance function and appearance; mathematicians have new arrangements to analyze and study; and artists can work together with scientists to perhaps make new works of art," he said.
Creating 'distinctly richer' tiling
It was already well known that two regular tetrahedra can be combined with a single regular
octahedron to tile or fill three-dimensional space. Buckminster Fuller, the renowned American architect, inventor and author who came into the mainstream consciousness when he designed geodesic dome-homes in the 1950s called such a structural relationship the "octet truss."
This type of tiling is ultimately related to a structure known as the face-centered cubic lattice, which is the densest possible arrangement of equal-sized non-overlapping spheres in space. By connecting the centers of spheres that are touching one another with lines, the resulting pattern of lines forms a lattice structure, Fuller's octet truss.
It was long believed that such a tiling and its closely related variants are the only tessellations of three-dimensional space that can be done with two different regular polyhedra.
Torquato and his colleagues' breakthrough is that they achieved that goal in a new way -- densely packing three-dimensional space, using one octahedron and six smaller tetrahedra. The resulting structure is what Torquato describes as a "distinctly different and richer" tiling, one that creates 694 separate concave repeat units, compared to two distinct repeat units in the face-centered cubic lattice. They also found an infinite variety of new tilings that span between this richer tiling and the octet-truss tiling.
In their work they essentially picked up where German mathematician Hermann Minkowski left off more than a century ago. Minkowski is credited with laying the mathematical groundwork for Einstein's theory of relativity. He used geometry-based methods to solve difficult problems in number theory.
Minkowski showed long ago that there is a way to pack octahedra densely. Minkowski also noted that such tiling left uniform holes shaped liked tetrahedra, but he did not recognize that these spaces had any particular significance. "If Minkowski had a computer, he probably could have figured out the significance of the holes," Torquato said.
Though the Princeton research was done strictly by using mathematics, the findings were rendered using computer graphics. The resulting images clearly showed how using four small tetrahedra and two larger ones could efficiently fill the space.
"This work is elegant in that it reveals packing modes that have been overlooked for years, specifically that the holes in lattices of optimal packings of octahedra are regular tetrahedra of equal size," said Michael Ward, a professor and chair of the Department of Chemistry at New York University. "Octahedra and tetrahedra may be regarded as simple objects themselves, which may suggest that unraveling their optimal packing modes would be straightforward. But this work illustrates that mathematical approaches, in this case, Torquato's polyhedron packing protocol, often can reveal patterns that are difficult, if not impossible, to visualize directly."
Ward added, "This work has the potential for broad impact in materials science, as material properties -- mechanical, optical, magnetic, electronic, to name a few -- hinge on the arrangement of individual constituents in the solid state."
Henry Cohn, a senior researcher at Microsoft Corp.'s theory group, called the team's discovery exciting.
"It sheds new light on [using] even the simplest building blocks for spatial structures," Cohn said. "Tetrahedra and octahedra are about as simple as it gets -- if you ignore cubes, which are the really obvious case -- but it's far from obvious how to combine them, and this paper shows that they can fill space in truly unexpected ways."
Deciphering the math behind tiling has intrigued intellectuals since Plato and led to much competition to be the first to solve some ancient numerical riddles. But Princeton's latest work on tiling is far more than a mathematical exercise, Torquato said. It has a variety of potential uses for physical and material sciences.
Architects have found tiling fascinating in part because it relates to the strength of structures. Tiling has also influenced artists and graphic designers because patterns can be visually arresting, even hypnotic, like the works of Dutch graphic artist M.C. Escher.
More recently, tiling has become important in managing data used to create computer graphics by computer scientists who structure that data into triangles.
"The world is filled with various nanoscopic building blocks and it often matters how they are organized," Torquato said.
The most obvious use is in materials science, where the newly discovered pattern could be used to create new materials, he said. Expanding on findings could lead to improved digital communications and better computer security.
The team's work was built on earlier findings detailed in a cover story in the journal Nature on Aug. 13, 2009, in which Torquato and Jiao described how to densely pack tetrahedra, octahedra and other polyhedra into space. The work was hailed as throwing out a new challenge to the math world. "That kind of stirred the pot," Torquato said, and his own group was among those that rose to the intellectual challenge. It took another two years to complete the work.
Provided by Princeton University