Mathematical model shows how groups split into factions

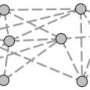
Social scientists have long argued that when under stress, social networks either end up all agreeing or splitting into two opposing factions. Either condition is referred to as "structural balance."

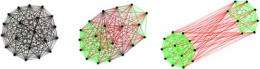
New Cornell research has generated a mathematical description of how this evolves. Previous mathematical approaches to structural balance have proven that when conditions are right, the result of group conflict will be a split into just two groups, the researchers said. The new work shows for the first time the steps through which friendships and rivalries shift over time and who ends up on each side.

This video is not supported by your browser at this time.

Watch the animation.

"Structural balance theory applies in situations where there's a lot of social stress -- gossip disparaging to one person, countries feeling pressure, companies competing -- where we need to make alliances and find our friends and enemies," said Cornell Ph.D. candidate Seth Marvel, lead author of a paper explaining the research published during the week of Jan. 3, 2011, in the online edition of the Proceedings of the National Academy of Sciences with co-authors Jon Kleinberg, the Tisch University Professor of Computer Science, Robert Kleinberg, assistant professor of computer science, and Steven Strogatz, the Jacob Gould Schurman Professor of Applied Mathematics.

People may form alliances based on shared values, or may consider the social consequences of allying with a particular person, Marvel said. "The model shows that the latter is sufficient to divide a group into two factions," he said.

The model is a simple differential equation applied to a matrix, or grid of numbers, that can represent relationships between people, nations or corporations. The researchers tested their model on a classic sociological study of a karate club that split into two groups and got results that matched what happened in real life. They plugged in data on international relations prior to World War II and got almost perfect predictions on how the Axis and Allied alliances formed.

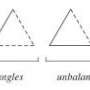
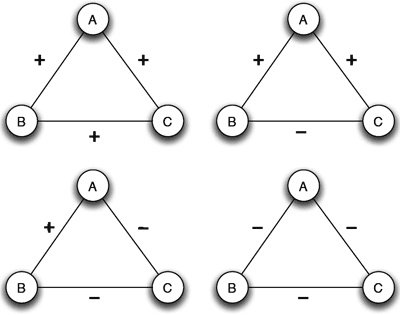
The smallest unit in such a network is a "relationship triangle," between, say, Bob and Carol and Ted, which can have four states:

• They're all good friends. That's a stable or "balanced" situation.


• Bob and Carol are friends, but neither gets along with Ted. That's also balanced.


• Bob and Carol dislike each other, but both are friends with Ted. Ted will try to get Bob and Carol together; he will either succeed or end up alienating one or both of his friends, so the situation is unbalanced and has a tendency to change.


• All three dislike each other. Various pairs will try to form alliances against the third, so this situation is also unbalanced.

"Every choice has consequences for other triangles," Strogatz explained, so unbalanced triangles kick off changes that propagate through the entire system. Too often the final state consists of two groups, each with all positive connections among themselves and all negative connections with members of the opposite group.

Social groups can be broken down to "relationship triangles" with four possibilities: A) A, B and C are mutual friends: balanced. B) A is friends with B and C, but they don't get along with each other: not balanced. C) A and B are friends with C as a mutual enemy: balanced. D) A, B, and C are mutual enemies: not balanced. Unbalanced triangles set off changes that spread through the group. From "Networks" by Jon Kleinberg and David Easley

Is there a way to avoid the mathematical certainty of a split, perhaps to make Republicans and Democrats in Congress less polarized? It depends on the initial conditions, Marvel said. The model shows that if the "mean friendliness" -- the average strength of connections across the entire network is positive, the system evolves to a single, all-positive pattern. "The model shows how to influence the result, but it doesn't tell you how to get there," Kleinberg cautioned.

Marvel plans to test the model on other social networks, and perhaps work with psychologists to do lab experiments with human subjects. But he too cautions against leaning too heavily on the equations for practical advice. "This is a simple model and deterministic, and people aren't deterministic," he said.

The research was supported in part by the John D. and Catherine T. MacArthur Foundation, Google, the Yahoo! Research Alliance, a Microsoft Research New Faculty Fellowship, the Air Force Office of Scientific Research and the National Science Foundation.

Provided by Cornell University