Random network connectivity can be delayed, but with explosive results, new study finds
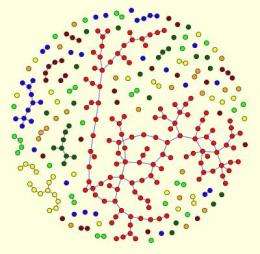
In the life of many successful networks, the connections between elements increase over time. As connections are added, there comes a critical moment when the network's overall connectivity rises rapidly with each new link.
Now a trio of mathematicians studying networks in which the formation of connections is governed by random processes, has provided new evidence that super-connectivity can be appreciably delayed. But the delay comes at a cost: when it finally happens, the transition is virtually instantaneous, like a film of water abruptly crystallizing into ice.
The team's findings — described in a paper with an accompanying commentary in the March 13 issue of the journal Science —could be useful in a number of fields: from efforts by epidemiologists to control the spread of disease, to communications experts developing new products.
"We have found that by making a small change in the rules governing the formation of a network, we can greatly manipulate the onset of large-scale connectivity," said Raissa D'Souza, an associate professor of mechanical and aeronautical engineering at UC Davis.
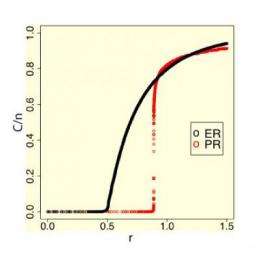
In the classic model of random network formation, known as the Erdös-Rényi model, connections are added from among a large collection of points one at a time by randomly selecting a pair of points to connect. Two points are considered to be in the same group if it is possible to go from one to another along a continuous line of connections. A group remains very small until the number of connections reaches at least half the number of points. After that, the growth of the largest group follows a steep upward curve.
D'Souza, along with co-investigators Dimitris Achlioptas at UC Santa Cruz and Joel Spencer at New York University, wanted to explore how a network would change if there were an element of choice injected into its formation. In their mathematical model, they considered two random connections in each step, and selected only one. To make their choice, they multiplied the number of points in the group linked to one end of a connection by the number of points linked to its other end. And in each case, they chose the connection that yielded the lower product.
As they expected, this process delayed the onset of super-connectivity. But the team's analysis provided strong evidence for a new phenomenon: when a system is suppressed like this, it builds up a kind of pressure. "This algorithm yields a very violent transition," Achlioptas said, "reaching a critical moment at which the probability that two points are connected jumps from essentially zero to more than 50 percent instantaneously."
Their calculations for this model have provided important insights that could be broadly applicable to understanding and influencing the behavior of various kinds of networks, D'Souza said, adding that the work should also spark a quest for a mathematical proof to back their findings, an endeavor that may require new mathematics.
"Consider this," she said. "Often we are presented with two alternatives, and must choose one. We have no control over which alternatives are presented, but we certainly can control what we choose."
Source: University of California - Davis